LitArk » Books » Romance novel

Krantz Steven G. - A Mathematical Odyssey Journey from the Real to the Complex

Here you can read online Krantz Steven G. - A Mathematical Odyssey Journey from the Real to the Complex full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Boston;MA, year: 2014, publisher: Springer US, genre: Romance novel. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
A Mathematical Odyssey Journey from the Real to the Complex
Author:
Krantz Steven G / Parks Harold R
Publisher:
Springer US
Genre:
Books / Romance novel
Year:
2014
City:
Boston;MA
Rating:
4 / 5
Favourites:
Add to favourites
Your mark:
- 80
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

A Mathematical Odyssey Journey from the Real to the Complex: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "A Mathematical Odyssey Journey from the Real to the Complex" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Mathematics is a poem. It is a lucid, sensual, precise exposition of beautiful ideas directed to specific goals. It is worthwhile to have as broad a cross-section of mankind as possible be conversant with what goes on in mathematics. Just as everyone knows that the Internet is a powerful and important tool for communication, so everyone should know that the Poincar conjecture gives us important information about the shape of our universe. Just as every responsible citizen realizes that the mass-production automobile was pioneered by Henry Ford, just so everyone should know that the P/NP problem has implications for security and data manipulation that will affect everyone. This book endeavors to tell the story of the modern impact of mathematics, of its trials and triumphs and insights, in language that can be appreciated by a broad audience. It endeavors to show what mathematics means for our lives, how it impacts all of us, and what new thoughts it should cause us to entertain. It introduces new vistas of mathematical ideas and shares the excitement of new ideas freshly minted. It discusses the significance and impact of these ideas, and gives them meaning that will travel well and cause people to reconsider their place in the universe. Mathematics is one of mankinds oldest disciplines. Along with philosophy, it has shaped the very modus of human thought. And it continues to do so. To be unaware of modern mathematics is to be miss out on a large slice of life. It is to be left out of essential modern developments. We want to address this point, and do something about it. This is a book to make mathematics exciting for people of all interests and all walks of life. Mathematics is exhilarating, it is ennobling, it is uplifting, and it is fascinating. We want to show people this part of our world, and to get them to travel new paths.

Krantz Steven G.: author's other books

Who wrote A Mathematical Odyssey Journey from the Real to the Complex? Find out the surname, the name of the author of the book and a list of all author's works by series.

A Mathematical Odyssey Journey from the Real to the Complex — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "A Mathematical Odyssey Journey from the Real to the Complex" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Steven G. Krantz and Harold R. Parks A Mathematical Odyssey 2014 Journey from the Real to the Complex 10.1007/978-1-4614-8939-9_1

Springer Science+Business Media New York 2014

1. The Four-Color Problem

Steven G. Krantz 1 and Harold R. Parks 2

(1)

Department of Mathematics, Washington University in St. Louis, St. Louis, MO, USA

(2)

Department of Mathematics, Oregon State University, Corvalis, OR, USA

Abstract

In 1852 Francis W. Guthrie, a graduate of University College London, posed the following question to his brother Frederick:

1.1 Humble Beginnings

In 1852 Francis W. Guthrie, a graduate of University College London, posed the following question to his brother Frederick:

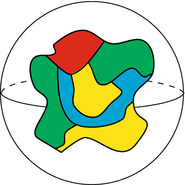
Imagine a geographic map on the earth (that is, on a sphere) consisting of countries onlyno oceans, lakes, rivers, or other bodies of water. The only rule is that a country must be a single contiguous massin one piece, and with no holessee Fig.). How many colors should the map-maker keep in stock in order to be sure he/she can color any map?

Figure 1.1

What is a country?

In fact, it was already known from experience that four colors suffice to color any map; the point was that no one had given a mathematical proof confirming the empirical observation.

Figure 1.2

A map coloring.

Frederick Guthrie was a student of the mathematician Augustus De Morgan (18061871), and he ultimately communicated the problem to his mentor. The problem was passed around among academic mathematicians for a number of years [in fact De Morgan communicated the problem to William Rowan Hamilton (18051865)]. The first allusion in print to the problem was by Arthur Cayley (18211895) in 1878.

These were all serious mathematicians, and it was rather surprising that such an elementary and accessible problem should prove so resistive to their best efforts. The problem became rather well known, and was dubbed The Four-Color Problem .

The eminent mathematician Felix Klein (18491925) in Gttingen heard of the problem and declared that the only reason the problem had never been solved is that no capable mathematician had ever worked on it. He , Felix Klein, would offer a class, the culmination of which would be a solution to the problem. He failed. Even so, Klein believed (and it was generally believed) that four colors would suffice to color any map. Certainly all the known examples pointed in that direction.

1.2 Kempe, Heawood, and the Chromatic Number

One reason the four-color problem is challenging is that one cannot simply piece together colorings of smaller maps to get a desired coloring of a bigger map. For instance, the map in Fig., then we will need to interchange some of the colors to avoid having a border with the same color on both sides. Similarly, if a new country is inserted somewhere in a four-colored map, then some of the existing colors may need to be changed to color the new map with only four colors.

Figure 1.3

A successful coloring.

Figure 1.4

Two four-colored maps needing recoloring before merging.

In 1879, Alfred Kempe (18451922) published what was believed to be a solution of the four-color problem. That is, he showed that any map on the earth (that is, the sphere) could be colored with four colors. Kempes proof turned out to be flawed, but it took 11years for anyone to discover the error.

Kempes argument involved first removing countries from the map in a carefully chosen order, then adding them back, recoloring the map as needed with each addition. The carefully chosen order was in fact designed to guarantee that each country that is added back borders no more than five countries. No recoloring is required if a reinserted country borders 1, 2, or 3 other countries, but it may be needed when the reinserted country borders 4 or 5 countries.

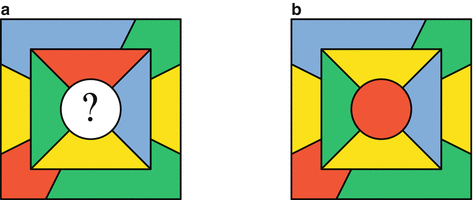
The first interesting case occurs when the reinserted country borders 4 existing countries and those countries have been colored using all four colors. The situation might be similar to that in Fig.b.

Figure 1.5

The easy case of adding back a country that borders all four colors ( a ) The initial coloring ( b ) After changing one red country to yellow, the new country can be colored red.

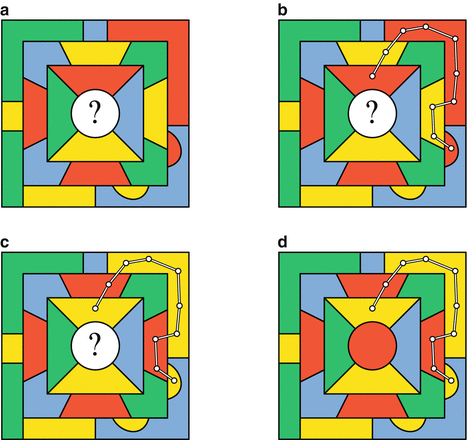
Kempes new idea was to extend this argument to more countries. For example, in Fig.a the new country is again surrounded by all four colors. None of the four surrounding colors can be changed individually, because each of those four countries also touches all three of the other colors.

Kempes procedure for coloring the new country relies on planning for many simultaneous color changes. Pick a pair of colors on opposite sides of the new country. We will pick red and yellow. Then, starting with the red country on top, form a larger set containing all the yellow countries it borders. Then include in the set all the red countries that those yellow countries border. Continue this process until no more countries get included. The set of countries just constructed is a Kempe chain . (Dont take the name chain too literallya Kempe chain is not necessarily a sequence, it may branch and/or contain contiguous clumps of countries.) Once the chain is formed, as in Fig.b, it is certainly harmless (i.e., introduces no countries sharing a border that are colored the same) to interchange the colors red and yellow in the Kempe chain.

There are now two cases:

(1)

The first possibility is that the Kempe chain does not include the country that is opposite the country that started the chainthat is the case in Fig.d.

Figure 1.6

Using a Kempe chain to add back a country that borders all four colors when the chain does not close up ( a ) The initial coloring ( b ) Form the Kempe chain ( c ) Change colors in the chain ( d ) Color the new country.

(2)

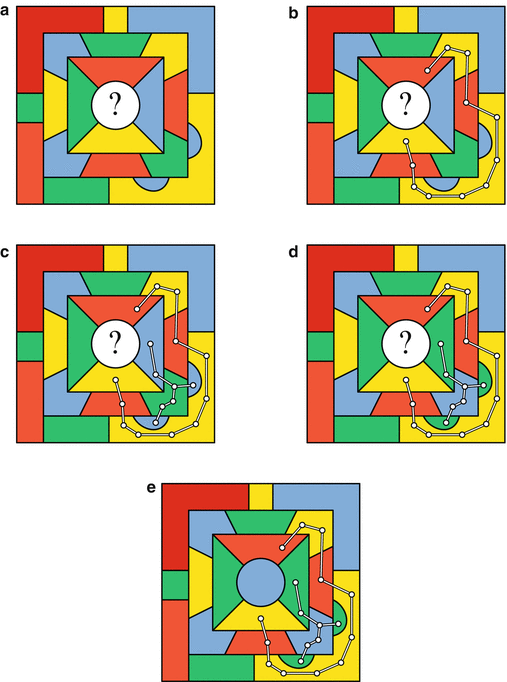
The second possibility is that the Kempe chain does include the country that is opposite the country that started the chain. This case is illustrated by the map in Fig.e.

Figure 1.7

Using a Kempe chain to add back a country that borders all four colors when the chain closes up ( a ) The initial coloring ( b ) Form the Kempe chain ( c ) Form a second chain ( d ) Change colors in the second chain ( e ) Color the new country.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «A Mathematical Odyssey Journey from the Real to the Complex»

Look at similar books to A Mathematical Odyssey Journey from the Real to the Complex. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Dietmar Herrmann

Ancient Mathematics: History of Mathematics in Ancient Greece and Hellenism

Pappas

The Magic of Mathematics: Discovering the Spell of Mathematics

Pappas

Mathematical footprints: discovering mathematics everywhere

Marcel Danesi

Pythagoras Legacy: Mathematics in Ten Great Ideas

Steven Krantz

Discrete Mathematics DeMYSTiFied

Alfred North Whitehead

An Introduction to Mathematics

W. W. Sawyer

Prelude to Mathematics

Donald Bindner

Mathematics for the Liberal Arts

Carl B. Boyer

A History of Mathematics

Theoni Pappas

The Magic of Mathematics: Discovering the Spell of Mathematics

Theoni Pappas

The Joy of Mathematics: Discovering Mathematics All Around You

Donal OShea

The Poincaré conjecture: in search of the shape of the universe

Reviews about «A Mathematical Odyssey Journey from the Real to the Complex»

Discussion, reviews of the book A Mathematical Odyssey Journey from the Real to the Complex and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.