Marcel Danesi - Pythagoras Legacy: Mathematics in Ten Great Ideas

The mathematics is not there till we put it there.

Sir Arthur Eddington (18821944)

Number rules the universe. These words were spoken in the 500s bce by one of historys most reclusive, yet most significant personages, the Ionian Greek philosopher Pythagoras of Samos. To examine the truth of his own aphorism, he founded a society, known as the Pythagorean Brotherhood, in the Greek colony of Crotone in southern Italy. The ideas the society came up withall in secretbecame the foundation of a new and exciting discipline, mathematics, devised as an intellectual tool for discovering the numbers that are hidden in the make-up of the universe. The term Pythagorean Brotherhood, which reflects a previous translation, is likely to be a misnomer, because Pythagoras encouraged women to participate fully in his society. Late in life, he married one of the members, Theano, who was an artist and healer. She took over leadership of the Pythagorean society after her husband, and even though she faced persecution, continued to spread Pythagoreanism throughout Egypt and Greece alongside her daughters.

The history of mathematics starts in earnest with one of Pythagoras most important proofsthe Pythagorean theorem. This proof was the first in a chain of ground-breaking ideas, all interconnected with each other, that turned mathematics into an art of the mind. That chain continues to be extended today. There would be no science, engineering, or philosophy without Pythagoras legacy. The purpose of this book is to sketch a history of that legacy by presenting and discussing ten of the greatest ideas in the mathematical chain. It aims to illustrate why mathematics can be designated an intellectual art, a creative enterprise that mirrors any art, from music to painting. Pythagoras actually connected music and mathematics into a system of knowledge that came to be called the Music of the Spheres.

This book is the result of teaching an undergraduate course on the history of puzzles at the University of Toronto for decades, a course for which mathematical ideas constitute its core. There are many varied and excellent histories of mathematics, but, as I discovered in teaching that course, only a few focus on how mathematical ideas are interconnected imaginatively. Pythagoras saw mathematics as existing outside of the human mind, constituting a secret code, as it may be called here, that might bear answers to the very question of existence. Whether true or not, it is something of which, I believe, everyone should be cognizant. The Hungarian writer Arthur Koestler (19051983) made the following relevant statement in his book, The Sleepwalkers (1959): Nobody before the Pythagoreans had thought that mathematical relations held the secret of the universe. Twenty-five centuries later, Europe is still blessed and cursed with their heritage. Needless to say, there are many other great ideas that I could have treated in this book. I chose these particular ones because they stand out consistently across histories of mathematics. They are also the ones that come up continually in my own course.

This book is intended both for those who love mathematics and those who do not. I hope to persuade the latter that mathematics is, well, more than math. For this reason, virtually no technical knowledge is required, since I have taken great care to ensure that everything is explained in plain language. Only basic high school mathematics is required. My goal is to show how mathematics can (and should) be envisioned as a creative art that is both pleasurable and understandable. As Mark Twain once wrote: Intellectual work is misnamed; it is a pleasure, a dissipation, and is its own highest reward (quoted in A Connecticut Yankee in King Arthurs Court, chapter 28, 1889). To make this book as enjoyable as possible, each of its ten chapters ends with five exploratory problems that will allow readers to become engaged in the main ideas treated in the chapter directly. Answers and explanations are found at the back of the book. There are fifty such explorations, allowing readers to use this book also as a collection of math problems.

I wish to express my gratitude to Daniel Taber and Katharine Ward for supporting this project and for their wonderful advice and suggestions. I am also thankful to Julian Thomas, for his superb work on this book. Any infelicities it may contain are my sole responsibility.

Marcel Danesi , 2019

University of Toronto

Fields Institute for Research in Mathematical Sciences

Reason is immortal, all else mortal.

Pythagoras (c. 580500 bce )

If we join a stick of length 3 inches, another one of 4 inches, and one more of 5 inches into a triangular shape, the result will be a right trianglea triangle in which one angle is a right angle (90). The same type of triangle, bigger in size, would result if we used sticks of lengths 5 inches, 12 inches, and 13 inches ().

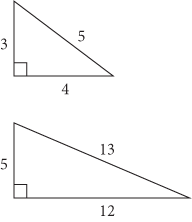
Figure 1.1 Right triangles

Any set of three random whole number lengths will not, however, necessarily produce such a triangle. The obvious question this raises is: Why do some three whole-number lengths, when combined, produce a right-angled triangle and others do not? The answer to this question is known as the Pythagorean theorem. It constitutes one of the first great ideas of mathematics. Its significance is evident in the fact that it has been taught in schools throughout human history; it has had many scientific applications; it has shown up in numerous other mathematical ideas; it is used commonly in engineering and construction problems; and the list could go on and on. In a phrase, it is one of those ideas that have mattered to human evolution. The goal of this opening chapter is to look at the theoremnamed after the ancient Greek mathematician, Pythagorasand at why it is so profoundly important.