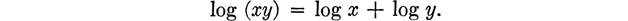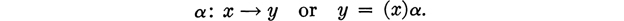The
THEORY
of
GROUPS
The
THEORY
of
GROUPS
Marshall Hall
DOVER PUBLICATIONS, INC.
MINEOLA, NEW YORK
Bibliographical Note
This Dover edition, first published in 2018, is an unabridged republication of the work originally published by The Macmillan Company, New York, in 1959.
Library of Congress Cataloging-in-Publication Data
Names: Hall, Marshall, 19101990, author.
Title: The theory of groups / Marshall Hall.
Description: Mineola, New York : Dover Publications, Inc., 2018. | Series: Dover books on mathematics | Reprint. Originally published by The Macmillan Company, New York, in 1959.
Identifiers: LCCN 2017034155| ISBN 9780486816906 (paperback) | ISBN 0486816907 (paperback)
Subjects: LCSH: Group theory. | BISAC: MATHEMATICS / Group Theory.
Classification: LCC QA171 .H27 2018 | DDC 512/.2dc23
LC record available at https://lccn.loc.gov/2017034155
Manufactured in the United States by LSC Communications
81690701 2018
www.doverpublications.com
DEDICATED TO
PHILIP HALL
PREFACE
The present volume is intended to serve a dual purpose. The first ten chapters are meant to be the basis for a course in Group Theory, and exercises have been included at the end of each of these chapters. The last ten chapters are meant to be useful as optional material in a course or as reference material. When used as a text, the book is intended for students who have had an introductory course in Modern Algebra comparable to a course taught from Birkhoff and MacLanes A Survey of Modern Algebra . I have tried to make this book as self-contained as possible, but where background material is needed references have been given, chiefly to Birkhoff and MacLane.
Current research in Group Theory, as witnessed by the publications covered in Mathematical Reviews is vigorous and extensive. It is no longer possible to cover the whole subject matter or even to give a complete bibliography. I have therefore been guided to a considerable extent by my own interests in selecting the subjects treated, and the bibliography covers only references made in the book itself. I have made a deliberate effort to curtail the treatment of some subjects of great interest whose detailed study is readily available in recent publications. For detailed investigations of infinite Abelian groups, the reader is referred to the appropriate sections of the second edition of Kuroschs Theory of Groups and Kaplanskys monograph Infinite Abelian Groups . The monographs Structure of a Group and the Structure of its Lattice of Subgroups by Suzuki and Generators and Relations for Discrete Groups by Coxeter and Moser, both in the Ergebnisse series, are recommended to the reader who wishes to go further with these subjects.
This book developed from lecture notes on the course in Group Theory which I have given at The Ohio State University over a period of years. The major part of this volume in its present form was written at Trinity College, Cambridge, during 1956 while I held a Fellowship from the John Simon Guggenheim Foundation. I give my thanks to the Foundation for the grant enabling me to carry out this work and to the Fellows of Trinity College for giving me the privileges of the College.
I must chiefly give my thanks to Professor Philip Hall of Kings College, Cambridge, who gave me many valuable suggestions on the preparation of my manuscript and some unpublished material of his own. In recognition of his many kindnesses, this book is dedicated to him.
I wish also to acknowledge the helpfulness of Professors Herbert J. Ryser and Jan Korringa and also Dr. Ernest T. Parker in giving me their assistance on a number of matters relating to the manuscript.
Marshall Hall, Jr.
Columbus, Ohio
CONTENTS
1. INTRODUCTION
1.1. Algebraic Laws.
A large part of algebra is concerned with systems of elements which, like numbers, may be combined by addition or multiplication or both. We are given a system whose elements are designated by letters a, b, c , . We write S = S ( a, b, c , ) for this system. The properties of these systems depend upon which of the following basic laws hold:
Closure Laws. | A 0. Addition is well defined . | M 0. Multiplication is well defined . |
These mean that, for every ordered pair of elements, a, b of S, a + b = c exists and is a unique element of S , and that also ab = d exists and is a unique element of S .
Associative Laws. | A 1. ( a + b ) + c = a + ( b + c ) | M 1. ( ab ) c = a ( bc ) |
Commutative Laws. | A 2. b + a = a + b | M 2. ba = ab |
Zero and Unit. | A 3. 0 exists such that 0 + a = a + 0 = a for all a . | M 3. 1 exists such that 1 a = a 1 = a for all a . |
Negatives and Inverses. | A 4. For every a , a exists such that ( a ) + a = a + ( a ) = 0. | M 4. For every a 0, a exists such that ( a ) a = a ( a ) = 1. |
Distributive Laws. | D 1. a ( b + c ) = ab + ac . | D 2. ( b + c ) a = ba + ca . |
D EFINITION : A system satisfying all these laws is called a field. A system satisfying A 0, 1, 2, 3, 4, M 0, 1, and D 1, 2 is called a ring .
It should be noted that A 0 A 4 are exactly parallel to M 0 M 4: except for the nonexistence of the inverse of 0 in M4. In the distributive laws, however, addition and multiplication behave quite differently. This parallelism between addition and multiplication is exploited in the use of logarithms, where the basic correspondence between them is given by the law:
In general an n -ary operation in a set S is a function f = f ( a , a n ) of n arguments ( a , a n ) which are elements of S and whose value f ( a , a n ) = b is a unique element of S when f is defined for these arguments. If, for every choice of a , a n in S, f ( a , a n ) is defined, we say that the operation f is well defined or that the set S is closed with respect to the operation f .
In a field F , addition and multiplication are well-defined binary operations, while the inverse operation f ( a ) = a is a unary operation defined for every element except zero.
1.2. Mappings,
A very fundamental concept of modern mathematics is that of a mapping of a set S into a set T .
D EFINITION : A mapping of a set S into a set T is a rule which as signs to each x of the set S a unique y of the set T . Symbolically we write this in either of the notations:
The element y is called the image of x under . If every y of the set T is the image of at least one x in S , we say that is a mapping of S onto T .
The mappings of a set into (or onto) itself are of particular importance. For example a rotation in a plane may be regarded as a mapping of the set of points in the plane onto itself. Two mappings and of a set S into itself may be combined to yield a third mapping of S into itself, according to the following definition.
D EFINITION : Given two mappings , , of a set S into itself, we define a third mapping of S into itself by the rule: If y = ( x ) and z = ( y ) , then z = ( x ) . The mapping is called the product of and , and we write = .