Paul Alexandroff - An Introduction to the Theory of Groups

Bibliographical Note

This Dover edition, first published in 2012, is an unabridged republication of the work originally published in 1959 by Blackie and Son, Ltd., London and Glasgow. That English translation was made from the German Einfhrung in die Gruppentheorie , published in 1954 by Deutscher Verlag der Wissenschaften, Berlin, which is itself a translation from the Russian of Paul Alexandroff by Lothar Uhlig.

Library of Congress Cataloging-in-Publication Data

Aleksandrov, P. S. (Pavel Sergeevich), 18961982.

[Vvedenie v teoriiu grupp. English]

An introduction to the theory of groups / Paul Alexandroff ; translated by Hazel Perfect and G.M. Petersen. Dover ed.

p. cm.

Originally published: London : Blackie, 1959.

Includes bibliographical references and index.

ISBN-13: 978-0-486-48813-4 (pbk.)

ISBN-10: 0-486-48813-6 (pbk.)

1. Group theory. 2. Catalysis. I. Title.

QA174.2.A43513 2012

512.2dc23

2011045172

Manufactured in the United States by Courier Corporation
48813601
www.doverpublications.com

The group concept has played a central part in the development of mathematical thought. At the same time, many aspects of the theory of groups are simple enough for the interested grammar school student to appreciate and absorb. We believe that this book by the eminent mathematician P. S. Alexandroff is especially suited for introducing the subject to the young student. The material presented is of fundamental importance and is developed in a clear and rigorous fashion, and the book is particularly noteworthy on account of the wealth of illustrative examples which are included.

We have added some exercises at the end of each chapter, and some references which we hope will be useful to the English-speaking student. We have also made a few minor alterations and additions to the actual text, some of which were made necessary by English usage, and we have corrected some minor errors.

Throughout the work we were able to consult Mrs. A. M. H. Marleyn over language obscurities, and we owe her a great debt of gratitude for the valuable and generous help which she gave us. We are also very grateful to Dr. H. O. Fouikes of the University College of Swansea for his critical reading of the text at the proof stage.

H. P.

G. M. P.

Next to the concept of a function, which is a most important concept pervading the whole of mathematics, the concept of a group is of the greatest significance in the various branches of mathematics and in its applications. The group concept is not any more difficult to appreciate than the function concept; indeed one can more easily become familiar with this concept during the early stages of a mathematical education than with the subject-matter of elementary mathematics.

Every pupil in a senior class of a grammar school who enjoys doing mathematics is capable of grasping the idea of a group if he is interested and industrious. And so this book has been written in the first place for the mathematically inclined pupils in the senior classes in the grammar school, but also for those who teach mathematics to the senior or to the advanced level. As regards the character of the exposition, I have been at pains to introduce no concepts without illustrating them by means of simple examples, for the most part geometrical.

P. S. A.

The addition of whole numbers satisfies the following conditions, which we call axioms of addition and which are of very great importance for all that follows:

I. Two numbers can be added together (i.e. to any two arbitrary numbers a and b there corresponds a uniquely determined number, which we call their sum: a + b ).

II. The Associative Law:

For any three arbitrary numbers a , b , c we have the following identity

III. Among the numbers there is a uniquely determined number 0, the zero, which is such that for every number a the relation

is satisfied .

IV. To every number a there corresponds a so-called inverse ( or negative ) number a, which has the property that the sum a + ( a ) is equal to zero:

Finally yet another important condition is satisfied.

V. The Commutative Law:

We show that it is possible to add not only numbers but also many other kinds of things, and that the above conditions remain satisfied.

First Example .We consider all possible rotations of an equilateral triangle ABC about its centroid 0 (). We see without difficulty that of all possible rotations of the triangle only three rotations send it into coincidence with itself, namely, the rotations through 120, 240, and the so-called zero rotation, which leaves all the vertices unchanged and hence also all the sides of the triangle. The first rotation sends the vertex A into the vertex B, the vertex B into the vertex C, the vertex C into the vertex A (we say that it permutes cyclically the vertices A, B, C). The second rotation sends A into C, B into A, C into B, and therefore permutes A,C,B cyclically.

Fig. 1

Now we introduce the following natural definition: The addition of two rotations means their successive application, the first rotation followed by the second. If we add the rotation through 120 to itself, then the result is the rotation through 240; if we add to it the rotation through 240, then the result is the rotation through 360, the zero rotation. Two rotations through 240 result in the rotation through 480 = 360 + 120; their sum is therefore the rotation through 120. If we denote the zero rotation by a 0, the rotation through 120 by a 1, the rotation through 240 by a 2, then we obtain the following relations:

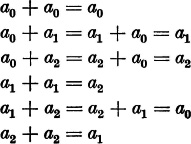
Thus the sum of any two of the rotations a 0, a 1, a 2 is defined and is again one of the rotations a 0, a 1, a 2 We easily convince ourselves that this addition satisfies the associative law and evidently also the commutative law. Further, there exists among these rotations a 0, a 1, a 2 a zero rotation a 0 which satisfies the condition

for every rotation a .

Finally each of the three rotations has an inverse, which when added to the original rotation produces the zero rotation. The zero rotation is evidently inverse to itself: a 0 = a 0, since a 0 + a 0 = a 0; further a 1 = a 2 and a 2 = a 1 (since a 1 + a 2 = a 0). Therefore addition of those rotations of an equilateral triangle, bringing the triangle into coincidence with itself, satisfies all the axioms of addition listed above.