Stefan Odenbach - Magnetic Hybrid-Materials: Multi-scale Modelling, Synthesis, and Applications

The design of hybrid materials that can be manipulated by magnetic fields is possible by incorporating inorganic magnetic nanoobjects into complex soft matrices such as gels [] in a predetermined way. A proper setup allows the application of external magnetic fields to either analyze or alter the material properties of such systems on a nanoscopic scale. The resulting hybrid structures have promising responsive properties that can be categorized into applications of interest either for actuation or sensing.

The fascinating prospective arising from magnetic nanoparticles dispersed in liquids (ferrofluids) [

The magnetic probe particles are further useful nanoscopic magnetic tracers, allowing the investigation of the nanoparticle interaction with their surrounding matrix by using dynamic magnetic methods on small sample volumes in a nondestructive way [].

Research of this kind strongly benefits from new developments in the controlled synthesis of prospective tracer particles with improved uniformity, stability, controlled surface characteristics, and novel coupling mechanisms [], the interaction between the probe or actuator particles and their environment can be tailored in wide limits.

The flow properties of complex fluids, as generally investigated by rheology, are relevant for the processing and application properties of all kinds of products in daily life, such as cosmetics and food. A broad spectrum of rheological methods is available for their assessment, spanning a large range of time and size regimes as well as measuring geometries.

The employment of microscopic approaches for the investigation of complex fluids is often related to the application of small tips or particles as probes. While passive methods, like particle tracking microscopy [.

The strong size-dependent properties that are measured in nanorheological experiments on microstructured samples make this method a promising candidate for the development of a method capable of determining local rheological properties on a nanoscale. The use of magnetically blocked, nanoscopic particles as tracers under the influence of an oscillating magnetic field is a particularly promising approach. The response of the particles in terms of their magnetic susceptibility is recorded, and in analogy to classical macrorheology, the phase shift of the response signal delivers information on the complex susceptibility and thus on the frequency-dependent excitation of the particle rotation.

The magnetic nanoparticles (MP) that are used as probes in this approach ideally need to fulfill a number of requirements in order to facilitate a simple and meaningful data analysis. In order to result in a direct correlation of the magnetic susceptibility data and the hydrodynamic characteristics of the probes, it is important to make sure that they are well-dispersed in the sample material on a single-particle level in a nonagglomerated way, and that no significant adsorption of matrix components on the particle surface occurs. Further, it is beneficial if the size distribution is narrow, and the basic magnetic properties, such as the magnetic moment, of each individual particle are uniform. Finally, the magnetic anisotropy is required to be high enough to ensure that the particles are magnetically blocked and accordingly relax predominantly by Brownian rotation [].

Among the particle systems suitable for application as tracers in MNP, magnetically blocked, single domain cobalt ferrite (CoFe2O4) nanoparticles, as shown in ].

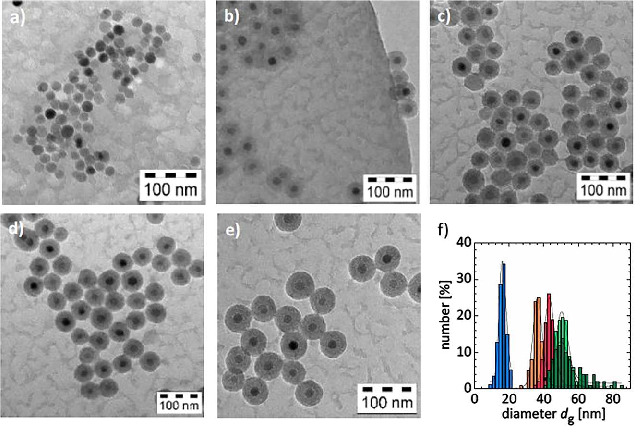
Figure 1.1: TEM images of tracer particles of the same magnetic core size and varying SiO2 shell thickness of a) 12 nm; b) 25 nm; c) 29 nm; d) 37 nm; and e) 42 nm. In f) the size distribution of the geometrical diameter d g with corresponding log normal function is shown for the different probe particles (a) (blue); b) (orange); c) (red); d) (light green); e) (green)). Reproduced by permission of the PCCP Owner Societies from [].

A suitable experimental setup is based on AC susceptometry. In a typical experiment, the sample is placed between a pair of excitation coils, while two pairs of detection coils are employed, one measuring the sample and the other measuring a blank. By amplification of the subtracted signals using a lock-in amplifier, the complex susceptibility is accessible. During the measurement a sinusoidal AC magnetic field with small amplitude is applied, which can be varied in frequency. The alternating field activates the magnetic nanoparticles in the sample to a frequency-dependent relaxation behavior. This rotational relaxation process of the particles occurs against the effective sample viscosity that might be influenced by the probe size and might further depend on frequency.

The simplest model to describe the frequency-dependent response function of the particle is given by the Debye model where the real part and the imaginary part of the susceptibility are expressed as functions of the excitation frequency and the relaxation time of the particle [],

Here, n denotes the number density of particles and m is the particles magnetic moment. For thermally blocked MP, the Brownian relaxation is dominant, and hence the corresponding relaxation time is accessible from a fit of the experimental data according to the Debye model. By application of the well-known Stokes-Einstein equation the obtained relaxation time B is related to the viscosity of the medium, the hydrodynamic radius of the particle