SOLVED PROBLEMS IN ANALYSIS
As Applied to Gamma, Beta, Legendre and Bessel FunctionsOrin J. Farrell Union College
Bertram Ross New Haven College
 Copyright
Copyright Copyright 1963 by Orin J. Farrell and Bertram Ross Copyright renewed 1991 by Mabel W. Farrell, James A. Farrell, William M.
Bibliographical Note This Dover edition, first published in 1971 and reissued in 2013, is an unabridged and corrected republication of the work originally published by the Macmillan Company in 1963 under the title:
Solved Problems: Gamma and Beta Functions, Legendre Polynomials, Bessel Functions.Library of Congress Cataloging-in-Publication Data Farrell, Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J.
Farrell, Bertram Ross. pages cm. Originally published: New York: Macmillan, 1963, under title Solved problems: gamma and beta functions, Legendre polynomials, Bessel functions. Includes bibliographical references and index. eISBN-13: 978-0-486-78308-6 ISBN-10: 0-486-49390-3 1. 2. 2.
Gamma functionsProblems, exercises, etc. I. Ross, Bertram. II. Title. QA405.F3 2013
515.52dc23 2013014028 Manufactured in the United States by Courier Corporation
49390301 2013
www.doverpublications.com
PREFACE TO THE FIRST EDITION
This book consists of a selection of problems, each with a solution worked out in detail, dealing with the properties and applications of the Gamma function and the Beta function, the Legendre polynomials, and the Bessel functions.
For those problems which involved more than mere choice of a suitable formula and appropriate use thereof, we have often endeavored to present solutions with emphasis on the considerations raised by the following questions: How does one make a start in attacking the problem? What theorems and techniques from algebra, trigonometry, analytic geometry, calculus, and the theory of functions appear applicable so as to be likely to effect a solution? How and why does one proceed from one step to the next? What clues present themselves either in the statement of the problem or in the facts which develop as the attempt at solution proceeds? What aspects of the problem must be carefully considered so that the solution will meet the demands of mathematical rigor? Such an approach usually leads to solutions that are neither brief nor elegant. We earnestly hope, however, that the lack of brevity and elegance is compensated by what may be called a naturalness of procedure combined with a heuristic presentation that make the solutions relatively easy to follow. We hope also that the solutions presented will be found stimulating, and that they will help to develop skill in attacking and solving problems in pure and applied mathematics. Cursory examination of this book might give the impression of an occasional haphazard choice of problem. But no problem was originated or chosen at random. Selection of problems was made so as to fulfill such purposes as exposition of suitable techniques of procedure and reasonable coverage of relevant topics.
Often a problem that seems out of place in one of the chapters on the properties of the functions ( are put to use in the chapters on applications. References to individual texts or treatises have been used sparingly in the statements of the problems and in the solutions. However, a modest bibliography of works typical of those one would find it profitable to consult is included at the end of the book. We gratefully make the following acknowledgments: were reprinted with the permission of The Royal Society and the American Institute of Electrical Engineers. We appreciate especially the excellent constructive criticisms and suggestions made by Dr.
PREFACE TO THE DOVER EDITION
We have been pleased at the response to this text from students who are studying applied classical analysis for the first time, and by professors who are not only looking for ways to motivate but also for ways to bring difficult subject matter down to an understandable level.
PREFACE TO THE DOVER EDITION
We have been pleased at the response to this text from students who are studying applied classical analysis for the first time, and by professors who are not only looking for ways to motivate but also for ways to bring difficult subject matter down to an understandable level.
In this Dover edition, we have endeavored to correct errors in the first edition, some of which were discovered by our students. We also appreciate the very careful reading given by Professor Yoshio Matsuoka, Kagoshimashi.
I
THE GAMMA FUNCTION AND THE BETA FUNCTION
INTRODUCTION
The Gamma function was first defined in 1729 by the great Swiss mathematician Euler. He defined the Gamma function by an infinite product:
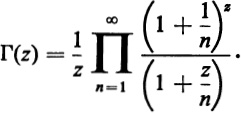
If
z be taken as the complex variable
x +
iy, Eulers product for (
z) converges at every finite
z except
z = 0, 1, 2, 3, . The function defined by the product is analytic at every finite
z except for the singular points just mentioned. At each of the singular points, (
z) has a simple pole.
The notation (z) and the name Gamma function were first used by Legendre in 1814. From Eulers infinite product for (z) can be derived the formula 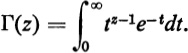 This integral formula is convergent only when the real part of z is positive. Nevertheless this integral formula for (z) often is taken as the starting point for introductory treatments of the Gamma function. Moreover, the variable z is often confined to real values x. So shall it be in this book: unless the contrary is explicitly stated, we shall be concerned in our exercises and problems with the Gamma function of a real variable only. For positive values of x we shall take the following as our basic definition of the Gamma function:
This integral formula is convergent only when the real part of z is positive. Nevertheless this integral formula for (z) often is taken as the starting point for introductory treatments of the Gamma function. Moreover, the variable z is often confined to real values x. So shall it be in this book: unless the contrary is explicitly stated, we shall be concerned in our exercises and problems with the Gamma function of a real variable only. For positive values of x we shall take the following as our basic definition of the Gamma function: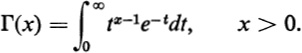 As is usually done, we shall extend the domain of the definition of the Gamma function into the realm of negative numbers (exclusive of negative integers) by extrapolation via the characteristic equation
As is usually done, we shall extend the domain of the definition of the Gamma function into the realm of negative numbers (exclusive of negative integers) by extrapolation via the characteristic equation 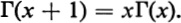 It may be remarked that this function, namely x(x), provides an analytic function whose value at each positive integer n is n!.
It may be remarked that this function, namely x(x), provides an analytic function whose value at each positive integer n is n!.
The Gamma function itself, as set up by Euler, is such that (n) = (n 1)! rather than n! when n is a positive integer, Although the Gamma function was devised by Euler to solve a problem in pure mathematics, here, as elsewhere in mathematics, an invention in pure mathematics has been found useful in applications of mathematics to problems in engineering and the sciences. The Gamma function is particularly useful in certain problems of probability, especially problems that involve factorials of large integers or the











 Copyright Copyright 1963 by Orin J. Farrell and Bertram Ross Copyright renewed 1991 by Mabel W. Farrell, James A. Farrell, William M. Bibliographical Note This Dover edition, first published in 1971 and reissued in 2013, is an unabridged and corrected republication of the work originally published by the Macmillan Company in 1963 under the title: Solved Problems: Gamma and Beta Functions, Legendre Polynomials, Bessel Functions.Library of Congress Cataloging-in-Publication Data Farrell, Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J.
Copyright Copyright 1963 by Orin J. Farrell and Bertram Ross Copyright renewed 1991 by Mabel W. Farrell, James A. Farrell, William M. Bibliographical Note This Dover edition, first published in 1971 and reissued in 2013, is an unabridged and corrected republication of the work originally published by the Macmillan Company in 1963 under the title: Solved Problems: Gamma and Beta Functions, Legendre Polynomials, Bessel Functions.Library of Congress Cataloging-in-Publication Data Farrell, Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J. [Solved problems] Solved problems in analysis: as applied to gamma, beta, Legendre and Bessel functions / Orin J. 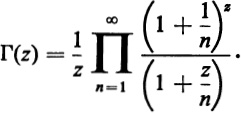 If z be taken as the complex variable x + iy, Eulers product for (z) converges at every finite z except z = 0, 1, 2, 3, . The function defined by the product is analytic at every finite z except for the singular points just mentioned. At each of the singular points, (z) has a simple pole.
If z be taken as the complex variable x + iy, Eulers product for (z) converges at every finite z except z = 0, 1, 2, 3, . The function defined by the product is analytic at every finite z except for the singular points just mentioned. At each of the singular points, (z) has a simple pole. 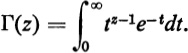 This integral formula is convergent only when the real part of z is positive. Nevertheless this integral formula for (z) often is taken as the starting point for introductory treatments of the Gamma function. Moreover, the variable z is often confined to real values x. So shall it be in this book: unless the contrary is explicitly stated, we shall be concerned in our exercises and problems with the Gamma function of a real variable only. For positive values of x we shall take the following as our basic definition of the Gamma function:
This integral formula is convergent only when the real part of z is positive. Nevertheless this integral formula for (z) often is taken as the starting point for introductory treatments of the Gamma function. Moreover, the variable z is often confined to real values x. So shall it be in this book: unless the contrary is explicitly stated, we shall be concerned in our exercises and problems with the Gamma function of a real variable only. For positive values of x we shall take the following as our basic definition of the Gamma function: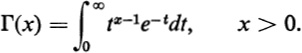 As is usually done, we shall extend the domain of the definition of the Gamma function into the realm of negative numbers (exclusive of negative integers) by extrapolation via the characteristic equation
As is usually done, we shall extend the domain of the definition of the Gamma function into the realm of negative numbers (exclusive of negative integers) by extrapolation via the characteristic equation 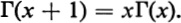 It may be remarked that this function, namely x(x), provides an analytic function whose value at each positive integer n is n!.
It may be remarked that this function, namely x(x), provides an analytic function whose value at each positive integer n is n!.