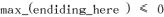A Collection of Dynamic Programming Interview Questions Solved in C++ Antonio Gulli Copyright 2014 Antonio Gulli All rights reserved. ISBN : 1495320480 ISBN-13 : 978-1495320484 Dynamic programming is the first of a series or 25 mini books devoted to algorithms, problem solving, and c++ programming DEDICATION To Lorenzo, my first child. With the hope that you will enjoy mathematics for the rest of your life, as much as you enjoyed solving problem 8 when you were 10 years old ACKNOWLEDGMENTS Thanks to Gaetan o Mendola for code reviewing Table of Contents
Dynamic programming: the art of solving simple problems first
Dynamic programming (DP) solves intricate problems by breaking them down into simpler components. DP can be applied to problems exhibiting two properties: overlapping subproblems and optimal substructure . Overlapping subproblems means that any recursive algorithm solving the problem should solve the same subproblems over and over, rather than generating new subproblems. Optimal substructure means that any optimal solution can be constructed efficiently from the optimal solutions of its subproblems.
In other words, suppose that each subproblem has its own cost function: the optimal substructure implies that the minima of each of these cost functions can be found as the minima of the global cost function restricted to the same subsets . DP pursues to solve each subproblem only once, as a result reducing the number of computations. After the solution to a given subproblem has been computed, it is stored in a table or "memoized". Next time the same solution is required, it is simply looked up. DP solves problems in either two methods: a) Top-down approach: This is a consequence of the recursive mathematical definition associated to many DP problems. b) Bottom-up approach: This requires a reformulation of the recursive mathematical definition where subproblems are solved first and their solutions used to build-on and achieve solutions for bigger subproblems In this book we will review a collection of Dynamic programming problems, their solution, and the C++ code related to them.
Many of those problems are commonly asked during interviews and can be frequently found on Internet web sites devoted to interviews preparation.
Fibonacci numbers
Solution The first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two. By describing the numbers in his book Liber Abaci , Leonardo Fibonacci introduced the sequence to Western European mathematics in 1200, although the sequence had been described earlier in Indian mathematics . Fibonacci numbers are mathematically defined as
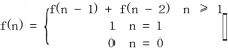
Code It is trivial to write a recursive solution directly derived from the mathematical formulation. Here we provide an implementation where Fibonacci is computed at compile time leveraging the power of templates. template < int N> struct CTFibonacci { static constexpr int value() { return CTFibonacci::value() + CTFibonacci::value(); } }; template <> struct CTFibonacci<1> { static constexpr int value() { return 1; } }; template <> struct CTFibonacci<0> { static constexpr int value() { return 0; } }; Complexity C omplexity is here exponential since
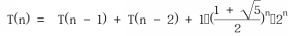
.
An alternative and more efficient solution memorizes the intermediate results and it avoids to recompute the same sub-problem for multiple times. A solution is: Code unsigned int Fibonacci( unsigned int n) { int a, b, sum; a = 0; b = 1; sum = a + b; if (n <= 1) return n; for ( unsigned int i = 2; i < n; ++i) { a = b; b = sum; sum = a + b; } return sum; } Complexity Linear in time and constant in space
Binomial Coefficient
The binomial coefficient indexed by
and
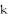
and denoted by
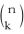
is the coefficient of the
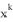
term in the polynomial expansion of the binomial power
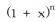
. The value of this coefficient is given by
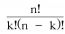
. Solution Computing the binomial coefficient directly from the closed formula
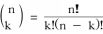
would be inefficient. However, we can prove by induction tha t
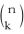
=
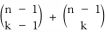
and we know that
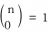
and
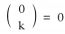
. Therefore, we have a direct way to compute the binomial coefficient with dynamic programming.
Note that Matrix is a class defined in the appendix. Code unsigned int bin( unsigned int n, unsigned int k, Matrix< int > & table) { std::cout << "n=" << n << " k=" << k << std::endl; if (n == 0) return 0; if (!table(n - 1, k - 1)) table(n - 1, k - 1) = bin(n - 1, k - 1, table); if (!table(n - 1, k)) table(n - 1, k) = bin(n - 1, k, table); return table(n - 1, k - 1) + table(n - 1, k); } unsigned int binomial( unsigned int n, unsigned int k) { if (k == 0) return 1; if (n == 0) return 0; Matrix< int > table(n + 1, k + 1, 0); for ( unsigned int i = 0; i <= n; i++) table(i , 0) = 1; return bin(n, k, table); } Complexity Linear in time 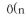 ). Space occupancy is
). Space occupancy is 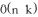
Max sub-array problem - given an array of integers, compute the largest sum continuous sub array
Solution This problem is a little gem. An elegant solution has been provided by Kadane. The key intuition for this algorithm is illustrated by this picture


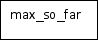
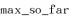
represents the maximum value computed before analysing the current subsequence, while
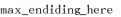
represents the maximum for the current subsequence. If
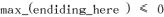 Next page
Next page






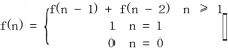 Code It is trivial to write a recursive solution directly derived from the mathematical formulation. Here we provide an implementation where Fibonacci is computed at compile time leveraging the power of templates. template < int N> struct CTFibonacci { static constexpr int value() { return CTFibonacci::value() + CTFibonacci::value(); } }; template <> struct CTFibonacci<1> { static constexpr int value() { return 1; } }; template <> struct CTFibonacci<0> { static constexpr int value() { return 0; } }; Complexity C omplexity is here exponential since
Code It is trivial to write a recursive solution directly derived from the mathematical formulation. Here we provide an implementation where Fibonacci is computed at compile time leveraging the power of templates. template < int N> struct CTFibonacci { static constexpr int value() { return CTFibonacci::value() + CTFibonacci::value(); } }; template <> struct CTFibonacci<1> { static constexpr int value() { return 1; } }; template <> struct CTFibonacci<0> { static constexpr int value() { return 0; } }; Complexity C omplexity is here exponential since 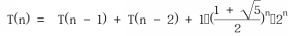 .
. 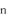 and
and 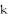 and denoted by
and denoted by 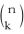 is the coefficient of the
is the coefficient of the 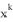 term in the polynomial expansion of the binomial power
term in the polynomial expansion of the binomial power 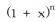 . The value of this coefficient is given by
. The value of this coefficient is given by 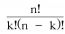 . Solution Computing the binomial coefficient directly from the closed formula
. Solution Computing the binomial coefficient directly from the closed formula 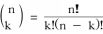 would be inefficient. However, we can prove by induction tha t
would be inefficient. However, we can prove by induction tha t 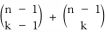 and we know that
and we know that 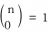 and
and 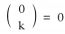 . Therefore, we have a direct way to compute the binomial coefficient with dynamic programming.
. Therefore, we have a direct way to compute the binomial coefficient with dynamic programming. 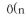 ). Space occupancy is
). Space occupancy is 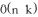


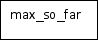
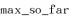 represents the maximum value computed before analysing the current subsequence, while
represents the maximum value computed before analysing the current subsequence, while 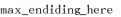 represents the maximum for the current subsequence. If
represents the maximum for the current subsequence. If