A collection of Bit Programming Interview Questions Solved in C++ Antonio Gulli Copyright 201 4 Antonio Gulli All rights reserved. ISBN: ISBN-13: Bits is the third of a series of 25 Chapters devoted to algorithms, problem solving, and C++ programming. DEDICATION To Leonardo, my second child. Hoping that you keep your curiosity and energy for the rest of your life. ACKNOWLEDGMENTS Thanks to Antonio Savona for his code review Contents
Given an unsigned int, swap the bits in odd and even positions
Solution
Assume that an unsigned int is 32bits and that we swap the bits in position
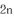
with those in position
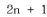
,
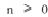
. In order to select all the even bits we can AND with bitmask 0xAAAAAAAAAA, which is a 32 bit number with even bits set (0xA is decimal 10, 1010 binary).
For selecting all the odd bits we can AND with bitmask 055555555, which is a number with all even bits sets (0x5 is decimal5, 0101 in binary). Then we need to shift left (respectively right) of one position and OR the two intermediate results.
Code
unsigned int swapBits( unsigned int x ) { unsigned int evenBits = x & 0xAAAAAAAA; unsigned int oddBits = x & 0x55555555; evenBits >>= 1; oddBits <<= 1; return (evenBits | oddBits); }
Print the binary representation of an unsigned int
Solution
An easy solution is to AND the
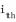
bit with the number
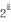
Code
void bin( unsigned n ) { for ( unsigned int i = 1 << 31; i > 0; i = i >> 1) if ( n & i) std::cout << 1; else std::cout << 0; }
Compute whether or not an unsigned number is a power of two
Solution
Suppose that the number is nonzero. If it is a power of two, than the only bit set is in position
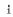
. In this case we subtract 1, so all the bits at the left of
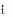
will be unset. Therefore a positive number
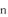
is a power of 2 if and only if
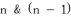
is 0.
Note that this check only works if 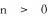
Code
bool isPowerOfTwo(unsigned n) { return n && (!(n & (n - 1))); }
Set the i-th bit
Solution
For a given number n we can set the i-th bit with the expression
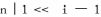
Unset the i-th bit
Solution
For a given number n we can unset the i-th bit with the expression
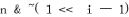
Toggle the i-th bit
Solution
For a given number n we can toggle the i-th bit with the expression
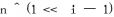
Given an unsigned number with only one bit set, find the position of this bit
Solution
If there is only one bit set, then the number must be a power of two. For identifying the position set we can AND the number with an appropriate bitmask.
Code
unsigned int findPosition( unsigned int n ) { unsigned int i = 1, pos = 1; while (!(i & n )) { i = i << 1; ++pos; } return pos; }
Solution
Another solution is using the logarithm for returning the position of the only bit set in the given unsigned
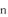
. The code returns -1 if
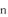
is not a power of 2.
Code
int findPosition2( unsigned int n ) { if ( n & ( n - 1)) return -1; return ( unsigned int )(log(( double ) n ) / log(2.0)) + 1; }
Solution
Yet another solution runs in
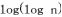
.
Code
int findPosition3( unsigned int n ) { if ( n & ( n - 1)) return -1; if ( n == 1 << 31) return 32; unsigned int position = 16; unsigned int half = 1 << 15; unsigned int stride = 16; while (1) { if ( n == half) return position; else if ( n > half) { n = n >> stride; position = position + (stride >> 1); } else { n = n & ((1 << stride) - 1); position = position - (stride >> 1); } half = half >> (stride >> 1); stride >>= 1; } return position; }
Count the number of bits set in an unsigned number
Solution
We can simply loop and count the bits with complexity
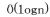
, where
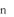
is the number of bits in the unsigned.
Code
unsigned int countBits( unsigned int n ) { unsigned int count = 0; while ( n ) { count += n & 1; n >>= 1; } return count; }
Solution for sparse bitmaps
This solution works better for sparse unsigned s because it runs in a time proportional to the number of bits set to 1.
Code
unsigned int countBits( unsigned int n ) { unsigned int count = 0; while ( n ) { count += n & 1; n >>= 1; } return count; }
Solution for sparse bitmaps
This solution works better for sparse unsigned s because it runs in a time proportional to the number of bits set to 1.
The line n &= (n 1) sets the rightmost 1 in the bitmap to 0.
Code
unsigned int countBitsSparse( unsigned int n ) { unsigned int count = 0; while ( n ) { count++; n &= ( n - 1); } return count; }
Solution for dense bitmaps
This solution works better for dense bitmaps because it runs in a time proportional to the number of bits set to 0. First you must toggle all the bits and then subtract the numbers of the set bits from
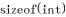
. The line n &= (n 1) sets the rightmost 1 in the bitmap to 0.
Code
unsigned int countBitsDense( unsigned int n ) { unsigned int count = 8 * sizeof ( unsigned int ); n = ~ n ; while ( n ) { count--; n &= ( n - 1); } return count; }
Solution for 32bit integers
This solution works better for unsigned 32 bits integers. Here you use an additional lookup table containing the number of 1s enclosed in the binary representation of the 8 bit
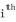
number.
Using pre-computed lookup tables is a commonly adopted trick for speeding up operations on lookup tables.
Code
static int bitInChar[256]; void fillBitsInChar() { for ( unsigned int i = 0; i < 256; ++i) bitInChar[i] = countBits(i); } unsigned int countBitsConstantFor32BitsInt( unsigned int n ) { return bitInChar[ n & 0xffu] + bitInChar[( n >> 8) & 0xffu] + bitInChar[( n >> 16) & 0xffu] + bitInChar[( n >> 24) & 0xffu]; }
Next page




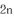 with those in position
with those in position 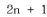 ,
, 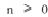 . In order to select all the even bits we can AND with bitmask 0xAAAAAAAAAA, which is a 32 bit number with even bits set (0xA is decimal 10, 1010 binary).
. In order to select all the even bits we can AND with bitmask 0xAAAAAAAAAA, which is a 32 bit number with even bits set (0xA is decimal 10, 1010 binary). 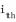 bit with the number
bit with the number 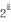
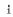 . In this case we subtract 1, so all the bits at the left of
. In this case we subtract 1, so all the bits at the left of 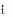 will be unset. Therefore a positive number
will be unset. Therefore a positive number 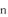 is a power of 2 if and only if
is a power of 2 if and only if 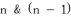 is 0.
is 0. 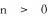
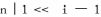
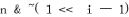
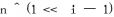
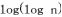 .
. 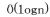 , where
, where 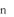 is the number of bits in the unsigned.
is the number of bits in the unsigned. 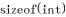 . The line n &= (n 1) sets the rightmost 1 in the bitmap to 0.
. The line n &= (n 1) sets the rightmost 1 in the bitmap to 0.  number.
number.