A collection of Tree Programming Interview Questions Solved in C++ Antonio Gulli Copyright 2015 Antonio Gulli All rights reserved. ISBN: ISBN-13: Tree is the fifth of a series of 25 Chapters devoted to algorithms, problem solving and C++ programming. DEDICATION To my wife Francesca Love always finds a path between forgiveness and karma ACKNOWLEDGMENTS Table of Contents
Implementing a preorder visit for a Binary Tree
Solution
A binary tree is a tree where every node has at most two children. The non-recursive pre-order visit can be implemented by using a stack. In a loop:
- First the current node is visited.
- Then the left children are pushed until a leaf is reached
- Then if the stack is empty, we leave the loop.
Implementing an in-order visit for a Binary Tree
Solution
A non-recursive in-order visit can be implemented by using a stack.
Implementing an in-order visit for a Binary Tree
Solution
A non-recursive in-order visit can be implemented by using a stack.
In a loop:
- First the left children are pushed until a leaf is reached
- Then if the stack is empty, we leave the loop. Otherwise the top of the stack pops out and the current node is visited.
- Finally the visit continues towards the right children
Code
template < typename tVal > void nonRecursiveInOrder( binaryTree < tVal > * root ) { std:: stack < binaryTree < tVal > *> s; while ( true ) { //left while ( root ) { s.push( root ); root = root ->left; } if (s.empty()) break ; // this one root = s.top(); s.pop(); std::cout << " v=" << root ->v__; //right root = root ->right; } }
Complexity
Time complexity is
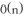
and space complexity is
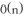
Implementing a post-order visit for a Binary Tree
Solution
During post-ordering every single node is visited twice: the first time when moving towards the left children and then again, when moving towards the right children. In order to differentiate the two cases, we can compare if the current element and the right child of the element at the top of the stack are the same.
Code
template < typename tVal > void nonRecursivePostOrder( binaryTree < tVal > * root ) { std:: stack < binaryTree < tVal > *> s; while ( true ) { if ( root ) { s.push( root ); root = root ->left; } else { if (s.empty()) break ; else if (!s.top()->right) { root = s.top(); s.pop(); std::cout << " v=" << root ->v__; if ( root == s.top()->right) { std::cout << " v=" << s.top()->v__; s.pop(); } } if (!s.empty()) root = s.top()->right; else root = NULL ; } // else } // while }
Complexity
Time complexity is
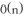
and space complexity is
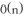
Implementing a level order visit for a Binary Tree
Solution
Level order visits can be implemented for all nodes at one level before going to the next level. The idea is very simple.
Counting the number of leaves in a tree
Solution
A solution can be provided by modifying the level order visit where we increment a counter every time we reach a leaf node.
Code
template < typename tVal > unsigned NumLeavesNonRecursiveLevelOrder( binaryTree < tVal > * root ) { std:: queue < binaryTree < tVal > *> q; binaryTree < tVal > * tmp; unsigned count = 0; if (! root ) return count; q.push( root ); while (!q.empty()) { tmp = q.front(); q.pop(); if (!tmp->left && !tmp->right) count++; // another leaf else { if (tmp->left) q.push(tmp->left); if (tmp->right) q.push(tmp->right); } } return count; }
Complexity
Time complexity is
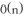
and space complexity is
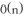
.
Checking if two binary trees are structurally identical
Solution
A solution can be provided by recursion.
Checking if two binary trees are structurally identical
Solution
A solution can be provided by recursion.
We consider as base cases when both nodes are null, or if only one of them is null. Otherwise the algorithm checks if both nodes contain the same value and if both left children and right children are recursively structurally identical.
Code
template < typename tVal > unsigned structIdentical( binaryTree < tVal > * r1 , binaryTree < tVal > * r2 ) { if (! r1 && ! r2 ) return true ; if (! r1 || ! r2 ) return false ; return ( r1 ->v__ == r2 ->v__ && structIdentical( r1 ->left, r2 ->left) && structIdentical( r1 ->right, r2 ->right));
}
Complexity
Time complexity is
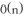
and space complexity is
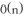
.
Printing all the paths in a binary tree
Solution
A solution can be provided by recursion. The idea is to keep a vector
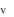
passing during recursion, while every node is pushed_back() to

.
Code
template < typename tVal > void printAllPaths( binaryTree < tVal > * root , std:: vector < tVal > path ) { if (! root ) return ; path .push_back( root ->v__); if (! root ->left && ! root ->right) { std:: vector < tVal >::iterator it = path.begin(); for (; it != path .end(); it++) std::cout << " v=" << *it; std::cout << std::endl; } else { printAllPaths( root ->left, path ); printAllPaths( root ->right, path ); } }
Complexity
Time complexity is
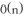
and space complexity is
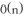
.
Verifying if a path sum is equal to an integer
Solution
The idea is to subtract the current value from the given sum, while visiting recursively the tree.
Code
template < typename tVal > bool hasSum( binaryTree < tVal > * root , int sum ) { if (! root ) return ( sum == 0); else { int remainingSum = sum - root ->v__; if (( root ->left && root ->right) || (! root ->left && ! root ->right)) return (hasSum( root ->left, remainingSum) || hasSum( root ->right, remainingSum)); else if ( root ->left) return hasSum( root ->left, remainingSum); else return hasSum( root ->right, remainingSum); } }
Complexity
Time complexity is
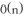
and space complexity is
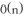
.
Find the maximum path sum between two leaves of a binary tree
Solution
The maximum path sum between two leaves can either touch the root of the three or can be located on a subtree only if it belongs to the tree itself.






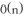 and space complexity is
and space complexity is 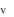 passing during recursion, while every node is pushed_back() to
passing during recursion, while every node is pushed_back() to  .
.