Joe Harris - Representation Theory

The primary goal of these lectures is to introduce a beginner to the finite-dimensional representations of Lie groups and Lie algebras. Since this goal is shared by quite a few other books, we should explain in this Preface how our approach differs, although the potential reader can probably see this better by a quick browse through the book.

Representation theory is simple to define: it is the study of the ways in which a given group may act on vector spaces. It is almost certainly unique, however, among such clearly delineated subjects, in the breadth of its interest to mathematicians. This is not surprising: group actions are ubiquitous in 20th century mathematics, and where the object on which a group acts is not a vector space, we have learned to replace it by one that is (e.g., a cohomology group, tangent space, etc.). As a consequence, many mathematicians other than specialists in the field (or even those who think they might want to be) come in contact with the subject in various ways. It is for such people that this text is designed. To put it another way, we intend this as a book for beginners to learn from and not as a reference.

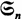This idea essentially determines the choice of material covered here. As simple as is the definition of representation theory given above, it fragments considerably when we try to get more specific. For a start, what kind of group G are we dealing witha finite group like the symmetric group or the general linear group over a finite field 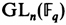, an infinite discrete group like SL n (), a Lie group like SL n , or possibly a Lie group over a local field? Needless to say, each of these settings requires a substantially different approach to its representation theory. Likewise, what sort of vector space is G acting on: is it over , , , or possibly a field of positive characteristic? Is it finite dimensional or infinite dimensional, and if the latter, what additional structure (such as norm, or inner product) does it carry? Various combinations of answers to these questions lead to areas of intense research activity in representation theory, and it is natural for a text intended to prepare students for a career in the subject to lead up to one or more of these areas. As a corollary, such a book tends to get through the elementary material as quickly as possible: if one has a semester to get up to and through Harish-Chandra modules, there is little time to dawdle over the representations of 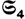and SL3.

By contrast, the present book focuses exactly on the simplest cases: representations of finite groups and Lie groups on finite-dimensional real and complex vector spaces. This is in some sense the common ground of the subject, the area that is the object of most of the interest in representation theory coming from outside.

The intent of this book to serve nonspecialists likewise dictates to some degree our approach to the material we do cover. Probably the main feature of our presentation is that we concentrate on examples, developing the general theory sparingly, and then mainly as a useful and unifying language to describe phenomena already encountered in concrete cases. By the same token, we for the most part introduce theoretical notions when and where they are useful for analyzing concrete situations, postponing as long as possible those notions that are used mainly for proving general theorems.

Finally, our goal of making the book accessible to outsiders accounts in part for the style of the writing. These lectures have grown from courses of the second author in 1984 and 1987, and we have attempted to keep the informal style of these lectures. Thus there is almost no attempt at efficiency: where it seems to make sense from a didactic point of view, we work out many special cases of an idea by hand before proving the general case; and we cheerfully give several proofs of one fact if we think they are illuminating. Similarly, while it is common to develop the whole semisimple story from one point of view, say that of compact groups, or Lie algebras, or algebraic groups, we have avoided this, as efficient as it may be.

It is of course not a strikingly original notion that beginners can best learn about a subject by working through examples, with general machinery only introduced slowly and as the need arises, but it seems particularly appropriate here. In most subjects such an approach means one has a few out of an unknown infinity of examples which are useful to illuminate the general situation. When the subject is the representation theory of complex semisimple Lie groups and algebras, however, something special happens: once one has worked through all the examples readily at handthe classical cases of the special linear, orthogonal, and symplectic groupsone has not just a few useful examples, one has all but five exceptional cases.

This is essentially what we do here. We start with a quick tour through representation theory of finite groups, with emphasis determined by what is useful for Lie groups. In this regard, we include more on the symmetric groups than is usual. Then we turn to Lie groups and Lie algebras. After some preliminaries and a look at low-dimensional examples, and one lecture with some general notions about semisimplicity, we get to the heart of the course: working out the finite-dimensional representations of the classical groups.

For each series of classical Lie algebras we prove the fundamental existence theorem for representations of given highest weight by explicit construction. Our object, however, is not just existence, but to see the representations in action, to see geometric implications of decompositions of naturally occurring representations, and to see the relations among them caused by coincidences between the Lie algebras.

The goal of the last six lectures is to make a bridge between the example-oriented approach of the earlier parts and the general theory. Here we make an attempt to interpret what has gone before in abstract terms, trying to make connections with modern terminology. We develop the general theory enough to see that we have studied all the simple complex Lie algebras with five exceptions. Since these are encountered less frequently than the classical series, it is probably not reasonable in a first course to work out their representations as explicitly, although we do carry this out for one of them. We also prove the general Weyl character formula, which can be used to verify and extend many of the results we worked out by hand earlier in the book.