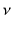Introduction
The study of particle motion in fluid flows relates to many different areas. In the atmosphere, small water droplets may form by condensation from vapor in the surrounding air and then continue to grow by sporadic collisions with other droplets, possibly forming precipitation (Shaw ). The droplets range in size from a few microns to a millimeter or so and are transported by the turbulent air flow while settling slowly under gravity. An atmospheric cloud of droplets may appear to be opaque but in fact the droplets are quite disperse with a volume fraction substantially less than
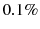
. The fluid (air) forces on the droplets create equal and opposite forces on the air flow and if the mass loading, i.e. the relative mass fraction of droplets in a given volume, is appreciable there can be a significant negative buoyancy on the flow. Since the density of water is about a thousand times that of air this can easily occur and leads to a sinking motion of the cloud and the surrounding air mass.
There is a general classification of dispersed two-phase, particle-laden flows based on the relative volume fraction and mass loading, see Balachandar and Eaton () and references therein. The combination of both low volume fraction and low mass loading gives one-way coupling. The overall flow is not modified by the particles, they essentially move in isolation, and they respond to fluid forces, such as drag, generated by their motion relative to the local ambient flow. Weak two-way coupling occurs if the overall flow is modified by the particles due to the mass loading but they are still sufficiently dispersed that the volume fraction remains low and they move in isolation with little fluid dynamic interaction between them. Full two-way coupling describes the general context of significant mass loading and volume fraction. One must then consider the particles and fluid as a collective system as in a suspension flow or a slurry flow, commonly involving solids in liquids. There are further classifications based on the size of the particle relative to the scale of the fluid motion and the Reynolds number associated with the particle motion.
There are numerous references covering the motion of particles in a range of interesting contexts. Guazzelli and Morris () give a review of turbidity currents and flows involving sediment transport in estuaries or coastal waters.
In this chapter, we first describe some of the ways to quantify the motion of isolated rigid particles considering mostly smaller spherical particles and the range of fluid forces that should be considered. We then consider the motion of these particles in simple laminar flows to illustrate how discrete particles differ from Lagrangian fluid tracers and some of the phenomena that may arise in nonuniform flows. In the subsequent sections we describe the force coupling method as a way to explore particle motion in more complex situations, including the effects of fluid interactions between particles and applications to suspension flows.
Motion of Isolated Particles
In the simplest situation a particle is so small that the viscous fluid forces, which scale with the surface area of the particle, are strong enough that there is no relative motion between the particle and the surrounding fluid. The particle then moves as a Lagrangian fluid element. The position
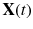
of such a fluid element in an incompressible flow
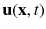
is then given by
This concept is the basis of particle image velocimetry (PIV) (Adrian and Westerweel ), where the flow is seeded with a sufficient number of small tracer particles to resolve the flow field but still maintaining a very low volume fraction and mass fraction. We assume that the effects of Brownian motion are negligible relative to the fluid forces and motion. The displacements of the PIV particles over short time intervals may then be used to measure the local fluid velocity. Further, these small spherical particles will rotate at an angular velocity
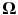
equal to half the local fluid vorticity
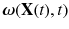
.
2.1 GasSolid Flows
The density of a solid particle is usually much larger than that of a gas and the effects of gravitational settling or particle inertia may be significant even if the particle is very small, essentially a point, relative to the scale of the surrounding flow. In the absence of a flow, a small but heavy particle will eventually fall at a terminal velocity
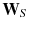
given by a balance of the fluid drag force in steady motion and the force of gravity. Buoyancy effects are negligible and using a Stokes drag law for a sphere of radius a (Batchelor ) the fluid force on a particle of mass
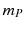
is,
where
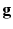
is the acceleration due to gravity and
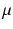
is the dynamic viscosity. A corresponding estimate may be made when the particle Reynolds number
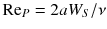
is non-zero and where
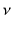













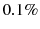 . The fluid (air) forces on the droplets create equal and opposite forces on the air flow and if the mass loading, i.e. the relative mass fraction of droplets in a given volume, is appreciable there can be a significant negative buoyancy on the flow. Since the density of water is about a thousand times that of air this can easily occur and leads to a sinking motion of the cloud and the surrounding air mass.
. The fluid (air) forces on the droplets create equal and opposite forces on the air flow and if the mass loading, i.e. the relative mass fraction of droplets in a given volume, is appreciable there can be a significant negative buoyancy on the flow. Since the density of water is about a thousand times that of air this can easily occur and leads to a sinking motion of the cloud and the surrounding air mass.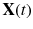 of such a fluid element in an incompressible flow
of such a fluid element in an incompressible flow 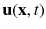 is then given by
is then given by 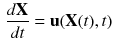
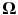 equal to half the local fluid vorticity
equal to half the local fluid vorticity 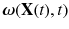 .
.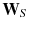 given by a balance of the fluid drag force in steady motion and the force of gravity. Buoyancy effects are negligible and using a Stokes drag law for a sphere of radius a (Batchelor ) the fluid force on a particle of mass
given by a balance of the fluid drag force in steady motion and the force of gravity. Buoyancy effects are negligible and using a Stokes drag law for a sphere of radius a (Batchelor ) the fluid force on a particle of mass 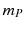 is,
is, 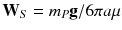
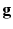 is the acceleration due to gravity and
is the acceleration due to gravity and 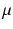 is the dynamic viscosity. A corresponding estimate may be made when the particle Reynolds number
is the dynamic viscosity. A corresponding estimate may be made when the particle Reynolds number 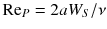 is non-zero and where
is non-zero and where