All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.
This book was set in Stone Serif by Westchester Publishing Services. Printed and bound in the United States of America.
Names: Rayo, Agustn, author.
Title: On the brink of paradox: highlights from the intersection of philosophy and mathematics / Agustn Rayo.
Description: Cambridge, MA: The MIT Press, [2019] | Includes bibliographical references and index.
Identifiers: LCCN 2018023088 | ISBN 9780262039413 (hardcover: alk. paper)
Subjects: LCSH: MathematicsProblems, exercises, etc. | Paradoxes. | Logic, Symbolic and mathematical.
Classification: LCC QA11.2.R39 2019 | DDC 510dc23 LC record available at https://lccn.loc.gov/2018023088
Contents
List of Figures
Levels of philosophical and mathematical demandingness corresponding to each chapter of the book.
Different paths through the book. A solid arrow from X to Y means that chapter X is presupposed by chapter Y; a dotted arrow means that reading chapter X before chapter Y could be helpful. Chapters closer to the top of the page are more desirable starting points, assuming you have no prior exposure to the material.
The non-negative rational numbers arranged on an infinite matrix. (Note that each number occurs infinitely many times, under different labels. For instance, 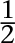 occurs under the labels
occurs under the labels 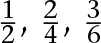 etc.)
etc.)
A path that goes through each cell of the matrix exactly once.
Notation for comparing the cardinality of infinite sets.
We are assuming the existence of a function f, which induces a complete list of real numbers in [0, 1).
An example of the list of real numbers in [0, 1) that might be induced by f.
A bijection from (0, 1) to .
The first few members of the ordinal hierarchy.
Ordinals are built in stages, with each stage bringing together everything previously introduced.
Each ordinal represents the well-order type that it itself instantiates under <o.
The eight possible hat distributions, along with the result of applying the suggested strategy.
A change in Georges timeline. The straight lines represent events as they originally occurred. The jagged line represents events as they occur after the change.
A is stationary; B is moving rightward at a constant speed.
A and B collide, exchanging velocities.
A wormhole in which the points represented by W- are identified with the points represented by W+. A jumps to the future when its spacetime trajectory reaches a point at which the wormhole is active; B jumps to the past when its spacetime trajectory reaches a spacetime point at which the wormhole is active.
There is no way of predicting how many particles will exist between W- and W+ using only information about time t.
After passing through point a and crossing through the wormhole at point b, particle A is reflected by a mirror at point c.
Particle A is prevented from entering the wormhole region by a future version of itself.
Particle A fails to enter the wormhole region after colliding with particle B at spacetime point a. Particles B and C are each caught in a loop within the wormhole.
In the above mosaic, neighboring cells are never colored alike. This pattern can determine, based on the color and location of any given cell, the color distribution of the rest of the mosaic. This means, in particular, that when the y-axis is thought of as a temporal dimension, with each row of the mosaic corresponding to one instant of time, the pattern can be used to characterize a deterministic law that determines, based on a specification of the mosaic at any given time, a full specification of the mosaic at every later time.
A resolution of the paradox with an extra particle, X.
Abbreviations from section 10.2.3.
Preface
Galileo Galileis 1638 masterpiece, Dialogues Concerning Two New Sciences, has a wonderful discussion of infinity, which includes an argument for the conclusion that the attributes larger, smaller, and equal have no place [] in considering infinite quantities (pp. 7780).
Galileo asks us to consider the question of whether there are more squares (12, 22, 32, 42, ) or more roots (1, 2, 3, 4, ). One might think that there are more roots on the grounds that, whereas every square is a root, not every root is a square. But one might also think that there are just as many roots as squares, since there is a bijection between the roots and the squares. (As Galileo puts it, Every square has its own root and every root has its own square, while no square has more than one root and no root has more than one square p. 78.)
We are left with a paradox. And it is a paradox of the most interesting sort. A boring paradox is a paradox that leads nowhere. It is due to a superficial mistake and is no more than a nuisance. An interesting paradox, on the other hand, is a paradox that reveals a genuine problem in our understanding of its subject matter. The most interesting paradoxes of all are those that reveal a problem interesting enough to lead to the development of an improved theory.
Such is the case of Galileos infinitary paradox. In 1874, almost two and a half centuries after Two New Sciences, Georg Cantor published an article that describes a rigorous methodology for comparing the sizes of infinite sets. Cantors methodology yields an answer to Galileos paradox: it entails that the roots are just as many as the squares. It also delivers the arresting conclusion that there are different sizes of infinity. Cantors work was the turning point in our understanding of infinity. By treading on the brink of paradox, he replaced a muddled pre-theoretic notion of infinite size with a rigorous and fruitful notion, which has become one of the essential tools of contemporary mathematics.
In part I of this book, Ill tell you about Cantors revolution (chapters 1 and 2) and about certain aspects of infinity that are yet to be tamed (chapter 3). In part II Ill turn to decision theory and consider two different paradoxes that have helped deepen our understanding of the subject. The first is the so-called Grandfather Paradox, in which someone attempts to travel back in time to kill his or her grandfather before the grandfather has any children (chapter 4); the second is Newcombs Problem, in which probabilistic dependence and causal dependence come apart (chapter 5). Well then focus on probability theory and measure theory more generally (chapters 6 and 7). Well consider ways in which these theories lead to bizarre results, and explore the surrounding philosophical terrain. Our discussion will culminate in a proof of the Banach-Tarski Theorem, which states that it is possible to decompose a ball into a finite number of pieces and then reassemble the pieces (without changing their size or shape) so as to get two balls, each the same size as the original (chapter 8).













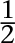 occurs under the labels
occurs under the labels 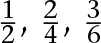 etc.)
etc.)