A. Lichnerowicz - Elements of Tensor Calculus

DOVER PUBLICATIONS, INC.

Mineola, New York

Bibliographical Note

This Dover edition, first published in 2016, is an unabridged republication of the translation of the 1958 4th edition originally published in 1962 by Methuen & Co. Ltd., London, and John Wiley & Sons, Inc., New York.

Library of Congress Cataloging-in-Publication Data

Names: Lichnerowicz, Andr, 1915-1998.

Title: Elements of tensor calculus / A. Lichnerowicz ; translated by J.W. Leech and D.J. Newman.

Other titles: Elements de calcul tensoriel. English

Description: Dover edition. | Mineola, New York : Dover Publications, Inc., 2016. | An unabridged republication of the 1962 translation of the 4th edition (1958); 1962 translation published by: London : Methuen & Co. Ltd.; New York : John Wiley & Sons, Inc. | Includes bibliographical references and index.

Identifiers: LCCN 2015047171| eISBN 9780486811864

Subjects: LCSH: Calculus of tensors. | Tensor fields. | Geometry, Differential.

Classification: LCC QA433 .L513 2016 | DDC 515/.63--dc23 LC record available at http://lccn.loc.gov/2015047171

Manufactured in the United States by RR Donnelley

80517401 2016

www.doverpublications.com

In 1900 Ricci and Levi-Civita produced a celebrated mmoire which gave the first systematic account of tensor calculus and drew the attention of mathematicians and physicists to some of its applications. Since then much has happened. The appearance of the theory of relativity, which would not have been possible without the previous existence of tensor calculus, gave it, in turn, an immense impetus. Tensor calculus has now become one of the essential techniques of modern theoretical physics. It has even been used recently in the study of technical problems such as the interconnection of electrical machines. It can be said that tensor calculus now forms a fundamental part of mathematics and physics.

This little book is divided into two parts, one concerned with tensor algebra and analysis, the other with the most important applications. In the study of tensor algebra ends with a brief consideration of outer product algebras, since this technique deserves to be better known by physicists. On the other hand, the concept of tensor density, which is of little mathematical interest, is not introduced. This concept is, in fact, easily avoided by the introduction of adjoint tensors of antisymmetric tensors.

In the chapters on tensor analysis I have confined myself to the analysis of tensor fields in Riemannian spaces, since Riemannian geometry is the most interesting from the point of view of applications. I have used systematically the method of transported reference frames due to M. lie Cartan. This method, which is the most geometrical and intuitive, has the added advantage of permitting the reader to avoid the consideration of other generalized geometries.

In the section on applications I was forced to be selective. The first chapter is intended to show the intuitive nature of Riemannian spaces in classical analytical dynamics and their usefulness in this field. In particular, an introduction to the study of continuous media and of elasticity is given. The reader wishing to extend his knowledge in this direction should refer to the excellent works of M. Lon Brillouin.

The remaining two chapters are devoted to the study of Maxwells equations of the electromagnetic field and to the theory of relativity. Only a brief sketch is given of the principles of general relativity theory. My task will have been accomplished if I have assisted the reader to undertake the study of the fundamental theories of contemporary physics.

In the course of translation some explanatory footnotes have been added and a number of references to works not available in English have been omitted. The Bibliography has been revised and extended in order to provide suitable suggestions for further reading.

Queen Mary College J. W. L.

(University of London) D. J. N.

1. Definition of a vector space. Consider the set of displacement vectors of elementary vector analysis. These satisfy the following rules:

(i) The result of vector addition of any two vectors, x and y, is their vector sum, or resultant, x + y. Vector addition has the following properties:

(a)x + y = y + x (commutative property);

(b)x + (y + z) = (x + y) + z (associative property);

(c)there exists a zero vector denoted by such that x + = x;

(d)for every vector x there is a corresponding negative vector (x), such that x + (x) = .

(ii) The result of multiplying a vector x by a real scalar is a vector denoted by x. Scalar multiplication has the following properties:

(a)1x = x;

(b)(x) = ()x (associative property);

(c)( + )x = x + x (distributive property for scalar addition);

(d)(x + y) = x + y (distributive property for vector addition).

Using the above properties as a guide, we now consider a general set E of arbitrary elements x, y etc., which obey the following rules:

(1) To every pairx, y, there corresponds an element x + y having the properties (a), (b), (c), (d).

(2) To every combination of an elementxand a real number there corresponds an elementxhaving the properties (a), (b), (c), (d).

We then say that E is a vector space over the field of real numbers and that the elementsx, y, etc., are vectors in E. If the second rule holds for all complex numbers a then E is a vector space over the field of complex numbers. Except when otherwise stated we shall confine ourselves in this book to the study of vector spaces over the field of real numbers.

2. Examples of vector spaces. There are several other simple examples of vector spaces which may be quoted to give an idea of the interest and application of the general concept.

(a) Consider the set of complex numbers a + ib, where a and b are real. The addition of any two complex numbers (a + ib, c + id, etc.) and the multiplication of a complex number by a real number obviously have the properties listed in . It follows that the set of complex numbers constitutes a vector space over the field of real numbers.

(b) Let X be an array of n real numbers arranged in definite order

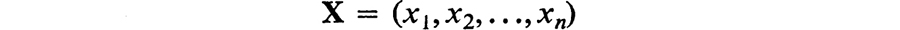
and let E be the set of all arrays X. Assume the following two rules of composition:

If X = (x1, x2, , xn) and Y = (y1, y2, , yn) then

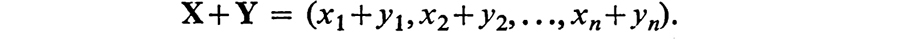
If X= (x1, x2, , xn