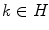Jean-Paul Penot Graduate Texts in Mathematics Calculus Without Derivatives 2013 10.1007/978-1-4614-4538-8_1
Springer Science+Business Media New York 2013
1. Metric and Topological Tools
Abstract
We devote this opening chapter to some preliminary material dealing with sets, set-valued maps, convergences, estimates, and well-posedness.
I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me .
Isaac Newton
We devote this opening chapter to some preliminary material dealing with sets, set-valued maps, convergences, estimates, and well-posedness.
A mastery of set theory (or rather calculus with standard operations dealing with sets) and of set-valued maps is necessary for nonsmooth analysis. In fact, one of the most attractive features of nonsmooth analysis consists in easy and frequent passages from sets to functions and vice versa. Moreover, several concepts of nonsmooth analysis become clear when one has some knowledge of set convergence. As an example, recall that the tangent to a curve C at some
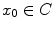
is defined as the limit of a secant passing through
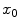
and another point x of C as
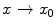
in C .
In this first chapter we gather some basic material that will be used in the rest of the book. Part of it is in standard use. However, we present it for the convenience of the reader. It can serve as a refresher for various notions used in the sequel; it also serves to fix notation and terminology. Thus, parts of it can be skipped by the learned reader. Still, some elements of the chapter are not so classical, although widely used in the field of nonsmooth analysis.
The most important results for further use are the Ekeland variational principle expounded in Sect.. These variational principles are such important tools for nonsmooth analysis that we already display some applications and present in supplements and exercises several variants of interest.
Among the direct consequences of smooth and nonsmooth variational principles are the study of conditioning of minimization problems, which is tied to the study of error bounds and sufficient conditions in order to get metric regularity. All these applications are cornerstones of optimization theory and nonsmooth analysis. For obtaining calculus rules, variational principles will be adjoined with penalization techniques in order to obtain decoupling processes. These techniques are displayed in Sects. and are rather elementary. These preparations will open an easy route to calculus. But the reader is already provided with tools that give precious information without using derivatives.
1.1 Convergences and Topologies
1.1.1 Sets and Orders
A knowledge of basic set theory is desirable for the reading of the present book, as in various branches of analysis. We assume that the reader has such a familiarity with the standard uses of set theory. But we recall here some elements related to orders, because Zorns lemma yields (among many other results) the HahnBanach theorem, which has itself numerous versions adapted to different situations.
Recall that a preorder or partial order or preference relation on a set X is a relation A between elements of X , often denoted by
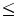
, with
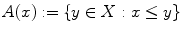
that is reflexive (
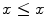
or
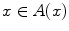
for all
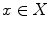
) and transitive (
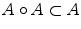
i.e.,
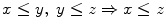
for
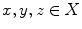
). One also writes
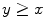
instead of
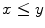
or
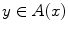
and one reads, y is above x or y is preferred to x . A preorder is an order whenever it is antisymmetric in the sense that
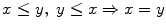
for every
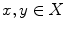
. Two elements x , y of a preordered set
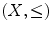
are said to be comparable if either
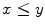
or
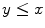
. If such is the case for all pairs of elements of X , one says that
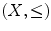
is totally ordered . That is not always the case (think of the set
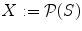
of subsets of a set S with the inclusion or of a modern family with the order provided by authority). Given a subset S of
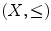
, an element m of X is called an upper bound (resp. a lower bound ) of S if one has
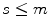
(resp.
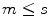
) for all s S . A preordered set ( I ,) is directed if every finite subset F of I has an upper bound. A subset J of a preordered set ( I ,) is said to be cofinal if for all i I there exists j J such that
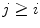
. A map
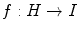
between two preordered spaces is said to be filtering if for all i I there exists
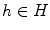
such that
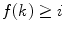
whenever
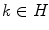












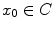 is defined as the limit of a secant passing through
is defined as the limit of a secant passing through 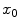 and another point x of C as
and another point x of C as 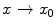 in C .
in C .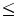 , with
, with 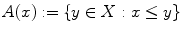 that is reflexive (
that is reflexive ( 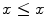 or
or 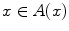 for all
for all 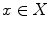 ) and transitive (
) and transitive ( 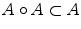 i.e.,
i.e., 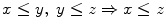 for
for 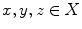 ). One also writes
). One also writes 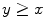 instead of
instead of 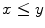 or
or 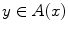 and one reads, y is above x or y is preferred to x . A preorder is an order whenever it is antisymmetric in the sense that
and one reads, y is above x or y is preferred to x . A preorder is an order whenever it is antisymmetric in the sense that 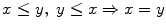 for every
for every 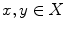 . Two elements x , y of a preordered set
. Two elements x , y of a preordered set 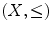 are said to be comparable if either
are said to be comparable if either 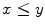 or
or 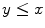 . If such is the case for all pairs of elements of X , one says that
. If such is the case for all pairs of elements of X , one says that 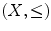 is totally ordered . That is not always the case (think of the set
is totally ordered . That is not always the case (think of the set 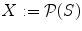 of subsets of a set S with the inclusion or of a modern family with the order provided by authority). Given a subset S of
of subsets of a set S with the inclusion or of a modern family with the order provided by authority). Given a subset S of 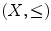 , an element m of X is called an upper bound (resp. a lower bound ) of S if one has
, an element m of X is called an upper bound (resp. a lower bound ) of S if one has 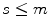 (resp.
(resp. 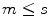 ) for all s S . A preordered set ( I ,) is directed if every finite subset F of I has an upper bound. A subset J of a preordered set ( I ,) is said to be cofinal if for all i I there exists j J such that
) for all s S . A preordered set ( I ,) is directed if every finite subset F of I has an upper bound. A subset J of a preordered set ( I ,) is said to be cofinal if for all i I there exists j J such that 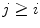 . A map
. A map 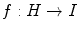 between two preordered spaces is said to be filtering if for all i I there exists
between two preordered spaces is said to be filtering if for all i I there exists 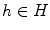 such that
such that 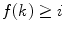 whenever
whenever