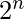GeeksForGeeks Engineering Mathematics Lecture Notes
From: https://www.geeksforgeeks.org/engineering-mathematics-tutorials/
Sum of squares of even and odd natural numbers
We know sum squares of first n natural numbers is n(n+1)(2n+1)/6.
How to compute sum of squares of first n even natural numbers?
We need to compute 22 + 42 + 62 + . + (2n)2
EvenSum = 22 + 42 + 62 + .... + (2n)2 = 4 x (12 + 22 + 32 + .... + (n)2) = 4n(n+1)(2n+1)/6 =
2n(n+1)(2n+1)/3Example
Sum of squares of first 3 even numbers = 2n(n+1)(2n+1)/3 = 2*3(3+1)(2*3+1)/3 = 5622 + 42 + 62 = 4 + 16 + 36 = 56
How to compute sum of squares of first n odd natural numbers?
We need to compute 12 + 32 + 52 + . + (2n-1)2
OddSum = (Sum of Squares of all 2n numbers) - (Sum of squares of first n even numbers) = 2n*(2n+1)*(2*2n + 1)/6 - 2n(n+1)(2n+1)/3 = 2n(2n+1)/6 [4n+1 - 2(n+1)] = n(2n+1)/3 * (2n-1) =
n(2n+1)(2n-1)/3Example:
Sum of squares of first 3 odd numbers = n(2n+1)(2n-1)/3 = 3(2*3+1)(2*3-1)/3 = 3512 + 32 + 52 = 1 + 9 + 25 = 35
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Engineering Mathematics
GATE CS
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Mean, Variance and Standard Deviation
Mean is average of a given set of data. Let us consider below example
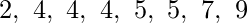
These eight data points have the mean (average) of 5:
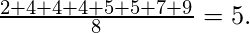
Variance is sum of squares of differences between all numbers and means.
Deviation for above example. First, calculate the deviations of each data point from the mean, and square the result of each:
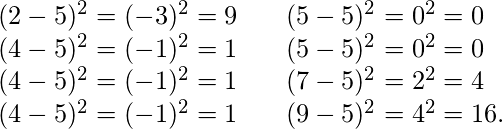
variance = 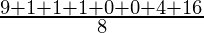 = 4.
= 4.
Standard Deviation is square root of variance. It is a measure of the extent to which data varies from the mean.
Standard Deviation (for above data) = 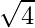 = 2
= 2
Why did mathematicians chose square and then square root to find deviation, why not simply take difference of values?
One reason is the sum of differences becomes 0 according to definition of mean. Sum of absolute differences could be an option, but with absolute differences it was difficult to prove many nice theorems. [Source: MIT Video Lecture at 1:19]
Some Interesting Facts:
1) Value of standard deviation is 0 if all entries in input are same.
2) If we add (or subtract) a number say 7 to all values in input set, mean is increased (or decreased) by 7, but standard deviation doesnt change.
3) If we multiply all values in input set by a number 7, both mean and standard deviation are multiplied by 7. But if we multiply all input values with a negative number say -7, mean is multiplied by -7, but standard deviation is multiplied by 7.
Below questions have been asked in previous year GATE exams
http://quiz.geeksforgeeks.org/gate-gate-cs-2012-question-64/
References:
https://en.wikipedia.org/wiki/Standard_deviation
http://staff.argyll.epsb.ca/jreed/math30p/statistics/standardDeviation.htm
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Engineering Mathematics
GATE CS
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Introduction of Set theory
A Set is a unordered collection of objects, known as elements or members of the set.
An element a belong to a set A can be written as a A, a A denotes that a is not an element of the set A.
Representation of a Set
A set can be represented by various methods. 3 common methods used for representing set:
1. Statement form.
2. Roaster form or tabular form method.
3. Set Builder method.
Statement form
In this representation, well defined description of the elements of the set is given. Below are some examples of same.
1. The set of all even number less than 10.
2. The set of number less than 10 and more than 1.
Roster form
In this representation, elements are listed within the pair of brackets {} and are separated by commas. Below are two examples.
1. Let N is the set of natural numbers less than 5.
N = { 1 , 2 , 3, 4 }.
2. The set of all vowels in english alphabet.
V = { a , e , i , o , u }.
Set builder form
In set builder set is describe by a property that its member must satisfy.
1. {x : x is even number divisible by 6 and less than 100}.
2. {x : x is natural number less than 10}.
Equal sets
Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.
NOTE: Order of elements of a set doesnt matter.
Subset
A set A is said to be subset of another set B if and only if every element of set A is also a part of other set B.
Denoted by .
A B denotes A is a subset of B.
To prove A is subset of B, we need to simply show that if x belongs to A then x also belongs to B.
To prove A is not a subset of B, we need find out one element which is part of set A but not belong to set B.
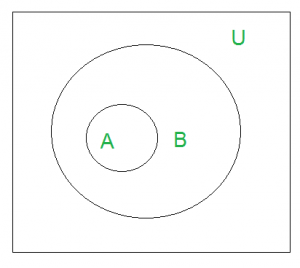
U denotes the universal set.
Above Venn Diagram shows that A is Subset of B.
Size of a Set
Size of a set can be finite or infinite.
For example
Finite set: Set of natural numbers less than 100.Infinite set: Set of real numbers.
Size of the set S is known as Cardinality number, denoted as |S|.
Example: Let A be a set of odd positive integers less than 10.
Solution : A = {1,3,5,7,9}, Cardinality of the set is 5, i.e.,|A| = 5.
Note: Cardinality of null set is 0.
Power Sets
Power set is the set all possible subset of the set S. Denoted by P(S).
Example : What is the power set of {0,1,2}?
Solution: All possible subsets
{}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.
Note : Empty set and set itself is also member of this set of subsets.
Cardinality of power set is
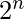
, where n is number of element in a set.
Cartesian Products
Let A and B be two sets. Cartesian product of A and B is denoted by A B, is the set of all ordered pairs (a,b), where a belong to A and B belong to B.
A B = {(a, b) | a A b B}.
Example 1. What is Cartesian product of A = {1,2} and B = {p,q,r}.









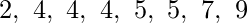
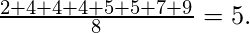
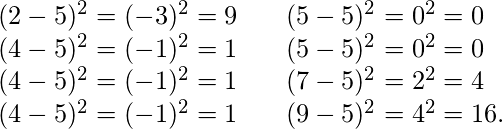
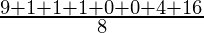 = 4.
= 4.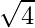 = 2
= 2