GeeksForGeeks Theory Of Computation and Automata Lecture Notes
From: https://www.geeksforgeeks.org/theory-of-computation-automata-tutorials/
Introduction of Theory of Computation
Automata theory (also known as Theory Of Computation) is a theoretical branch of Computer Science and Mathematics, which mainly deals with the logic of computation with respect to simple machines, referred to as automata.
Automata* enables the scientists to understand how machines compute the functions and solve problems. The main motivation behind developing Automata Theory was to develop methods to describe and analyse the dynamic behavior of discrete systems.
Automata is originated from the word Automaton which is closely related to Automation.
Now, lets understand the basic terminologies, which are important and frequently used in Theory of Computation.
- Symbol: Symbol is the smallest building block, which can be any alphabet, letter or any picture.

- Alphabets (): Alphabets are set of symbols, which are always finite.

- String: String is a finite sequence of symbols from some alphabet. String is generally denoted as w and length of a string is denoted as |w|.Empty string is the string with zero occurrence of symbols, represented as .Number of Strings (of length 2) that can be generated over the alphabet {a, b} - - - a a a b b a b bLength of String |w| = 2Number of Strings = 4Conclusion:For alphabet {a, b} with length n, number of strings can be generated = 2n.
Note If the number of s is represented by ||, then number of strings of length n, possible over is ||n.
- Language: A language is a set of strings, chosen form some * or we can say- A language is a subset of * . A language which can be formed over can be Finite or Infinite.

Powers of :
Say = {a,b} then
= Set of all strings over of length 0. {}
= Set of all strings over of length 1. {a, b}
= Set of all strings over of length 2. {aa, ab, ba, bb}
i.e. |2|= 4 and Similarly, |3| = 8
* is a Universal Set.* = 0 U 1 U 2 .......... = {} U {a, b} U {aa, ab, ba, bb} = ............. //
infinite language.
References
cs.stanford.edu
Wikipedia

abhishek1
WorKing to be bEst veRsion of MySelf
If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
GATE CS
Theory of Computation & Automata
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Chomsky Hierarchy
According to chomsky hierarchy, grammars are divided of 4 types:
Type 0 known as unrestricted grammar.Type 1 known as context sensitive grammar.Type 2 known as context free grammar.Type 3 Regular Grammar.
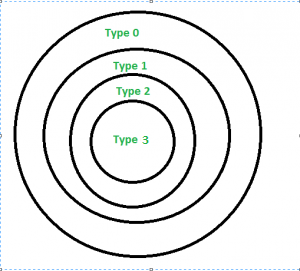
Type 0 ( Unrestricted Grammar )
In Type 0
Type-0 grammars include all formal grammars. Type 0 grammar language are recognized by turing machine. These languages are also known as the recursively enumerable languages.
Grammar Production in the form of
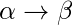
where
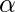 is ( V + T)* V ( V + T)*
is ( V + T)* V ( V + T)*
V : Variables
T : Terminals.
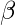 is ( V + T )*.
is ( V + T )*.
In type 0 there must be at least one variable on Left side of production.
For example,
Sab > ba
A > S.
Here, Variables are S, A and Terminals a, b.
Type 1 (Context Sensitive )
Type-1 grammars generate the context-sensitive languages. The language generated by the grammar are recognized by the Linear Bound Automata
In Type 1
1. First of all Type 1 grammar should be Type 0.
2. Grammar Production in the form of
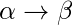
|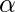 | <= |
| <= |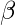 |
|
i.e count of symbol in 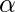 is less than or equal to
is less than or equal to 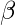
For Example,
S > AB
AB > abc
B > b
Type 2 ( Context Free )
Type-2 grammars generate the context-free languages. The language generated by the grammar is recognized by a Non Deterministic Push down Automata. Type-2 grammars generate the context-free languages.
In Type 2,
1. First of all it should be Type 1.
2. Left hand side of production can have only one variable.
|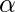 | = 1.
| = 1.
Their is no restriction on 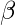 .
.
For example,
S > AB
A > a
B > b
Type 3 (Regular Grammar)
Type-3 grammars generate the regular languages.These languages are exactly all languages that can be decided by a finite state automaton.
Type 3 is most restricted form of grammar.
Type 3 should be in the given form only :
V > VT* / T*.
(or)
V > T*V /T*
for example :
S > ab.
REFERENCES
https://en.wikipedia.org/wiki/Chomsky_hierarchy
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Theory of Computation & Automata
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Finite Automata Introduction
Finite Automata(FA) is the simplest machine to recognize patterns.
A Finite Automata consists of the following :














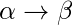
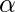 is ( V + T)* V ( V + T)*
is ( V + T)* V ( V + T)*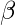 is ( V + T )*.
is ( V + T )*.