GeeksForGeeks Digital Electronics and Logic Design Lecture Notes
From: https://www.geeksforgeeks.org/digital-electronics-logic-design-tutorials/
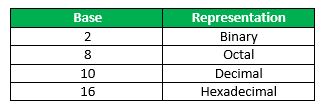
Number System and base conversions | Digital Electronics
Electronic and Digital systems may use a variety of different number systems, (e.g. Decimal, Hexadecimal, Octal, Binary).
A number N in base or radix b can be written as:
(N)b = dn-1 dn-2 d1 d0 . d-1 d-2 d-m
In the above, dn-1 to d0 is integer part, then follows a radix point, and then d-1 to d-m is fractional part.
dn-1 = Most significant bit (MSB)
d-m = Least significant bit (LSB)
How to convert a number from one base to another?
Follow the example illustrations:
1. Decimal to Binary
(10.25)10
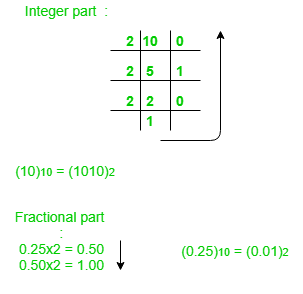
Note: Keep multiplying the fractional part with 2 until decimal part 0.00 is obtained.
(0.25)10 = (0.01)2
Answer: (10.25)10 = (1010.01)2
2. Binary to Decimal
(1010.01)2
123 + 0x22 + 121+ 0x20 + 0x2 -1 + 12 -2 = 8+0+2+0+0+0.25 = 10.25
(1010.01)2 = (10.25)10
3. Decimal to Octal
(10.25)10
(10)10 = (12)8
Fractional part:
0.25 x 8 = 2.00
Note: Keep multiplying the fractional part with 8 until decimal part .00 is obtained.
(.25)10 = (.2)8
Answer: (10.25)10 = (12.2)8
4. Octal to Decimal
(12.2)8
1 x 81 + 2 x 80 +2 x 8-1 = 8+2+0.25 = 10.25
(12.2)8 = (10.25)10
5. Hexadecimal and Binary
To convert from Hexadecimal to Binary, write the 4-bit binary equivalent of hexadecimal.
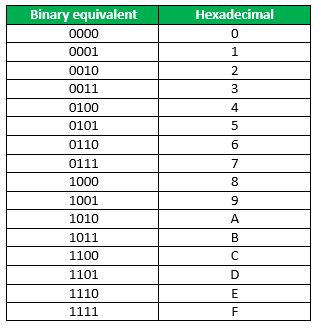
(3A)16 = (00111010)2
To convert from Binary to Hexadecimal, group the bits in groups of 4 and write the hex for the 4-bit binary. Add 0's to adjust the groups.
1111011011
(001111011011 )2 = (3DB)16
This article is contributed by Kriti Kushwaha.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Digital Electronics & Logic Design
base-conversion
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Floating Point Representation | Digital Logic
1. To convert the floating point into decimal, we have 3 elements in a 32-bit floating point representation:
i) Sign
ii) Exponent
iii) Mantissa
- Sign bit is the first bit of the binary representation. '1' implies negative number and '0' implies positive number.
Example: 11000001110100000000000000000000 This is negative number. - Exponent is decided by the next 8 bits of binary representation. 127 is the unique number for 32 bit floating point representation. It is known as bias. It is determined by 2k-1 -1 where 'k' is the number of bits in exponent field.
There are 2 exponent bits in 8-bit representation and 8 exponent bits in 32-bit representation.
Thus
bias = 3 for 8 bit conversion (22-1 -1 = 4-1 = 3)
bias = 127 for 32 bit conversion. (28-1 -1 = 128-1 = 127)
Example: 01000001110100000000000000000000
10000011 = (131)2
131-127 = 4
Hence the exponent of 2 will be 4 i.e. 24 = 16.
- Mantissa is calculated from the remaining 24 bits of the binary representation. It consists of '1' and a fractional part which is determined by:
Example:
01000001110100000000000000000000
The fractional part of mantissa is given by:
1*(1/2) + 0*(1/4) + 1*(1/8) + 0*(1/16) + = 0.625
Thus the mantissa will be 1 + 0.625 = 1.625
The decimal number hence given as: Sign*Exponent*Mantissa = (-1)*(16)*(1.625) = -26
2. To convert the decimal into floating point, we have 3 elements in a 32-bit floating point representation:
i) Sign (MSB)
ii) Exponent (8 bits after MSB)
iii) Mantissa (Remaining 23 bits)
- Sign bit is the first bit of the binary representation. '1' implies negative number and '0' implies positive number.
Example: To convert -17 into 32-bit floating point representation Sign bit = 1 - Exponent is decided by the nearest smaller or equal to 2n number. For 17, 16 is the nearest 2n. Hence the exponent of 2 will be 4 since 24 = 16. 127 is the unique number for 32 bit floating point representation. It is known as bias. It is determined by 2k-1 -1 where 'k' is the number of bits in exponent field.
Thus bias = 127 for 32 bit. (28-1 -1 = 128-1 = 127)
Now, 127 + 4 = 131 i.e. 10000011 in binary representation.
- Mantissa: 17 in binary = 10001.
Move the binary point so that there is only one bit from the left. Adjust the exponent of 2 so that the value does not change. This is normalizing the number. 1.0001 x 24. Now, consider the fractional part and represented as 23 bits by adding zeros.
00010000000000000000000
Thus the floating point representation of -17 is 1 10000011 00010000000000000000000
Related Link:
https://www.youtube.com/watch?v=03fhijH6e2w
More questions on number representation:
http://quiz.geeksforgeeks.org/number-representation/
This article is contributed by Kriti Kushwaha
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Digital Electronics & Logic Design
Please write to us at contribute@geeksforgeeks.org to report any issue with the above content.
Program for Binary To Decimal Conversion
Given a binary number as input, we need to write a program to convert the given binary number into equivalent decimal number.
Examples:
Input : 111Output : 7Input : 1010Output : 10Input: 100001Output: 33
Recommended: Please solve it on PRACTICE first, before moving on to the solution.
The idea is to extract the digits of given binary number starting from right most digit and keep a variable dec_value. At the time of extracting digits from the binary number, multiply the digit with the proper base (Power of 2) and add it to the variable dec_value. At the end, the variable dec_value will store the required decimal number.
For Example:
If the binary number is 111.
dec_value = 1*(2^2) + 1*(2^1) + 1*(2^0) = 7
Below diagram explains how to convert ( 1010 ) to equivalent decimal value:
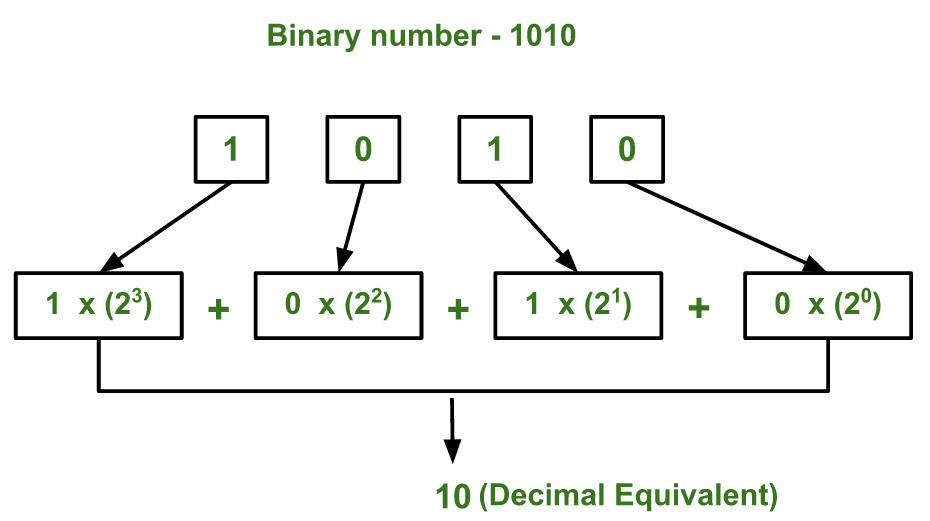
Below is the implementation of above idea :
C++
// C++ program to convert binary to decimal#includeusing namespace std;// Function to convert binary to decimalint binaryToDecimal(int n){ int num = n; int dec_value = 0; // Initializing base value to 1, i.e 2^0 int base = 1; int temp = num; while (temp) { int last_digit = temp % 10; temp = temp/10; dec_value += last_digit*base; base = base*2; } return dec_value;}// Driver program to test above functionint main(){ int num = 10101001; cout < <