De Gruyter Textbook
ISBN 9783110660388
e-ISBN (PDF) 9783110660395
e-ISBN (EPUB) 9783110660418
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
2021 Walter de Gruyter GmbH, Berlin/Boston
Mathematics Subject Classification 2010: 97I20, 97I60, 53A04, 53A05, 97N80,
Continuity of functions and mappings
In this book we shall deal with mappings from a subset URn to Rm for arbitrary positive integers m and n, where at least one of them is greater than one. Such mappings f are given as collections of m functions (f1,f2,,fm) , where fi:UR is a function of n variables. Usually, for m=1 , they are called functions and for m>1 mappings (maps, vector-valued functions).
In this chapter we first deal with Rn and introduce the notions of metric, norm, inner product, and discuss relations between them. Then we define the notions of limits, topology, and continuous mappings. We show how to visualize mappings in Mathematica and study their continuity. As an application we illustrate how continuous mappings can be used to analyze the topological properties of sets.
1.1 Metrics
Recall that a metric space is a set X together with a map d:XXR0 with the following properties [, p.650]:
d(x,y)=0 if and only if x=y ;
d(x,y)=d(y,x) ;
d(x,z)d(x,y)+d(y,z) (triangle inequality).
Mathematica has many built-in functions containing the word distance as one can check by typing
For instance, EuclideanDistance , HammingDistance , GraphDistance , TravelDistance , and many others. However, not all of them refer to a distance in our sense. The most general, applicable to any set X, is the function BinaryDistance :
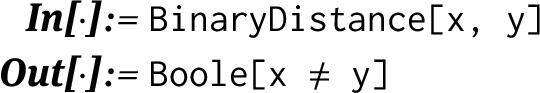 In this metric the distance between any element and itself is 0, and the distance between any unequal elements is 1. It is easy to verify the triangle inequality by hand. If we try to use Mathematica for this purpose, we obtain a somewhat strange result:
In this metric the distance between any element and itself is 0, and the distance between any unequal elements is 1. It is easy to verify the triangle inequality by hand. If we try to use Mathematica for this purpose, we obtain a somewhat strange result:
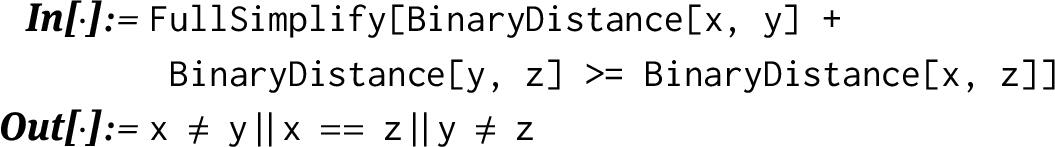 Of course, this relationship should evaluate to True . However, Mathematica cannot simplify such expressions unless it knows that the symbols represent real (or complex) numbers:
Of course, this relationship should evaluate to True . However, Mathematica cannot simplify such expressions unless it knows that the symbols represent real (or complex) numbers:
| In[]:= | FullSimplify[%, Assumptions -> Element[_, Reals]] |
| Out[]:= | True |
The most important distance for us will be the EuclideanDistance . It is normally defined on the Cartesian product Rn , but since Mathematica by default works over the complex numbers, it computes the distance in Cn :
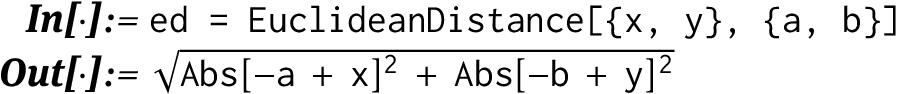 One way to deal with this is to apply the function ComplexExpand , which by default assumes that all parameters are real:
One way to deal with this is to apply the function ComplexExpand , which by default assumes that all parameters are real:
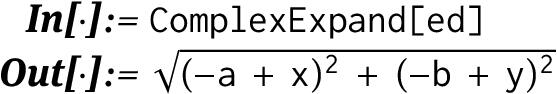 We can also use ComplexExpand to see that the distance on the set Cn is just the Euclidean distance on R2n :
We can also use ComplexExpand to see that the distance on the set Cn is just the Euclidean distance on R2n :
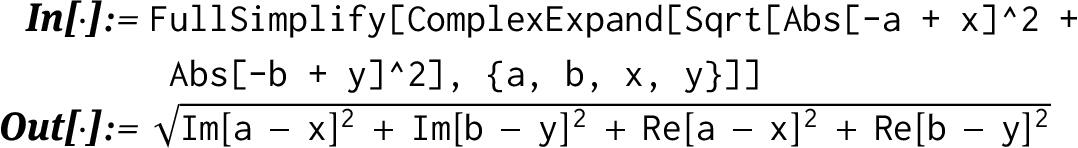 Note that ComplexExpand treats all variables as real unless they are listed in the second argument.
Note that ComplexExpand treats all variables as real unless they are listed in the second argument.
Other useful distances on Rn are ManhattanDistance and ChessboardDistance :
| In[]:= | ManhattanDistance[{x, y, z}, {a, b, c}] |
| Out[]:= | Abs[-a + x] + Abs[-b + y] + Abs[-c + z] |
| In[]:= | ChessboardDistance[{x, y, z}, {a, b, c}] |
| Out[]:= | Max[Abs[-a + x], Abs[-b + y], Abs[-c + z]] |
As can be seen from the above, the ManhattanDistance between two points is the sum of the distances between their projections on the coordinate axes, while the ChessboardDistance is the maximum of these distances. It is easy to show that both satisfy the triangle inequality.
A very important consequence of having a metric on a set X is that it defines a topology on X. In order to define a topology on X, we need the notion of an open set, and to define open sets, we need the notion of an open ball. The open ball with center at x0 of radius r>0 is the set B(x0,r)={xX|d(x,x0) . A subset YX is called a neighborhood of yY if there is an r>0 such that B(y,r)Y . A subset UX is said to be open if it is a neighborhood of its every point. Closed sets are the complements of open sets. Clearly, the empty set and the whole space X are both open and closed sets.
To understand open sets with respect to a metric, we need to understand the open balls. The following function draws a ball of a given radius for a given metric:
| In[]:= | ball[metric_, r_] := RegionPlot[metric[{x, y}, {0, 0}] |
| < r, {x, -2*r, 2*r}, {y, -2*r, 2*r}] |
Note that since RegionPlot never draws objects of dimension less than two, it will not correctly represent ball[BinaryDistance, 1] , which is a point (actually the picture is empty). Let us consider the balls in the following metrics:
| In[]:= | {ball[EuclideanDistance, 1], ball[ManhattanDistance, 1], |
| ball[ChessboardDistance, 1]} |
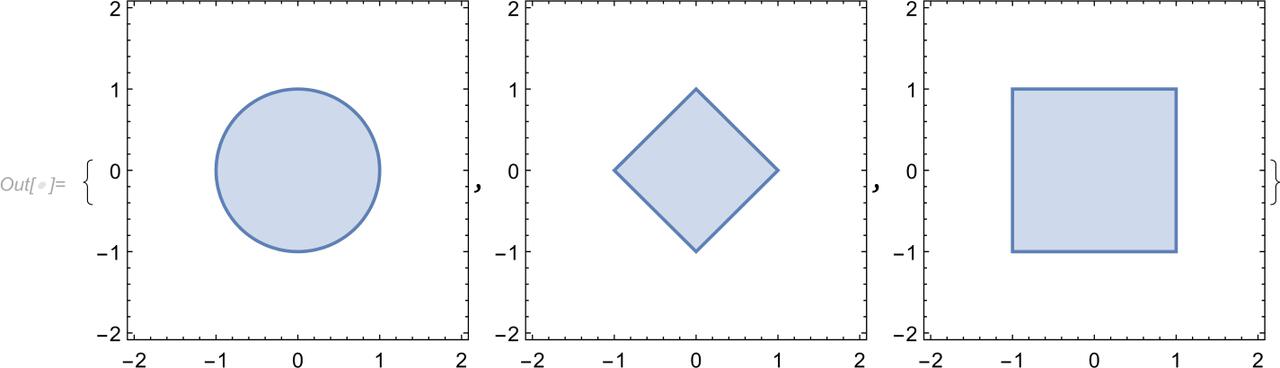
We can now see that although the open balls in these metrics have different shapes, a ball in each metric contains and is contained in a ball of any other metric:
| In[]:= | Show[(ball[#1[[1]], #1[[2]]] & ) /@ |
| {{EuclideanDistance, 1}, {ManhattanDistance, 1/2}, |
| {ChessboardDistance, 1/4}, {EuclideanDistance, 1/8}}] |
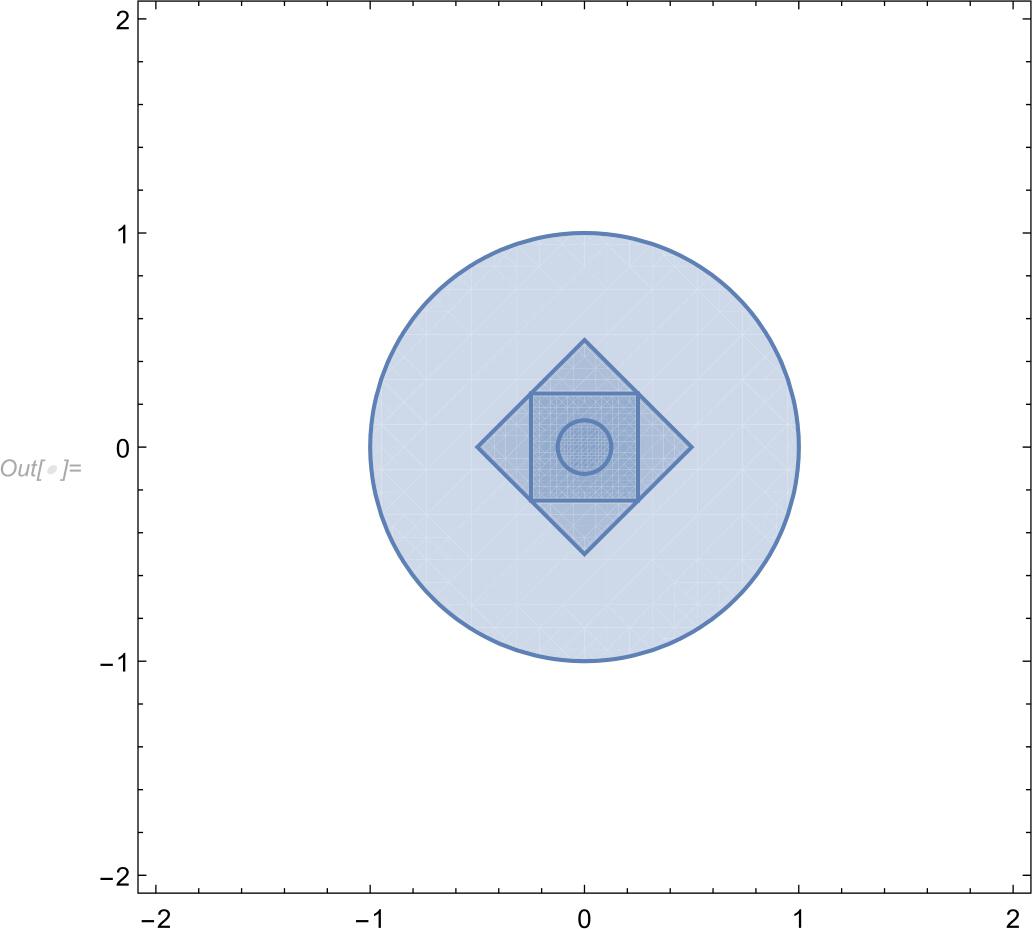
This implies that any open set with respect to any of these metrics is also open with respect to any other of these three metrics.
We say that two metrics d1 and d2 on X are equivalent if there exist constants c1>0 and c2>0 such that c1d1(x,y)d2(x,y)c2d1(x,y) for all x,yX . It is easy to see that all the metrics above are equivalent. Clearly, the binary metric is not equivalent to them.







![Chris Monahan [Chris Monahan] - Calculus II](/uploads/posts/book/119088/thumbs/chris-monahan-chris-monahan-calculus-ii.jpg)




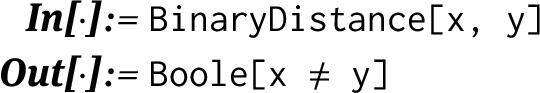 In this metric the distance between any element and itself is 0, and the distance between any unequal elements is 1. It is easy to verify the triangle inequality by hand. If we try to use Mathematica for this purpose, we obtain a somewhat strange result:
In this metric the distance between any element and itself is 0, and the distance between any unequal elements is 1. It is easy to verify the triangle inequality by hand. If we try to use Mathematica for this purpose, we obtain a somewhat strange result: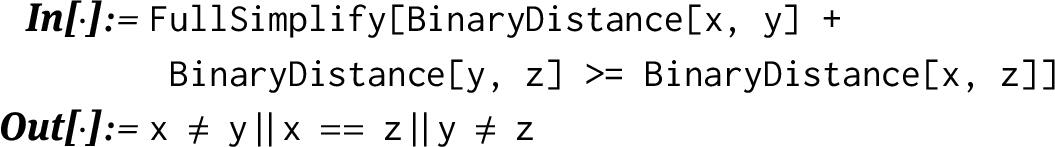 Of course, this relationship should evaluate to True . However, Mathematica cannot simplify such expressions unless it knows that the symbols represent real (or complex) numbers:
Of course, this relationship should evaluate to True . However, Mathematica cannot simplify such expressions unless it knows that the symbols represent real (or complex) numbers: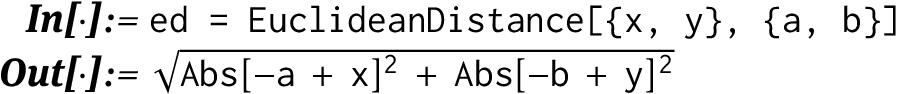 One way to deal with this is to apply the function ComplexExpand , which by default assumes that all parameters are real:
One way to deal with this is to apply the function ComplexExpand , which by default assumes that all parameters are real: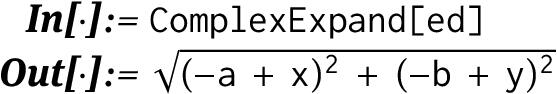 We can also use ComplexExpand to see that the distance on the set Cn is just the Euclidean distance on R2n :
We can also use ComplexExpand to see that the distance on the set Cn is just the Euclidean distance on R2n :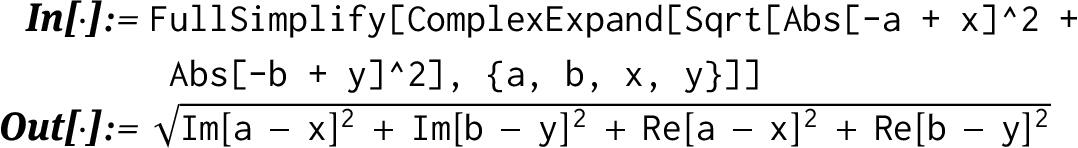 Note that ComplexExpand treats all variables as real unless they are listed in the second argument.
Note that ComplexExpand treats all variables as real unless they are listed in the second argument.
