Faye Anderson - Survival Analysis by Example: Hands on approach using R
Here you can read online Faye Anderson - Survival Analysis by Example: Hands on approach using R full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2016, publisher: UNKNOWN, genre: Computer. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Survival Analysis by Example: Hands on approach using R
- Author:
- Publisher:UNKNOWN
- Genre:
- Year:2016
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Survival Analysis by Example: Hands on approach using R: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Survival Analysis by Example: Hands on approach using R" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Faye Anderson: author's other books
Who wrote Survival Analysis by Example: Hands on approach using R? Find out the surname, the name of the author of the book and a list of all author's works by series.
Survival Analysis by Example: Hands on approach using R — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Survival Analysis by Example: Hands on approach using R" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
Survival Analysis by Example Hands on approach using R First Edition Faye Anderson, MS, PhD Contents Veritas
Preface
Last but not least, this book assumes basic knowledge of R. Code on how to import data, install a package, or save results can easily be obtained from the multitude of public sources in the internet. Enjoy!
Chapter 1: Survival Analysis Terminology
Survival time is greater or equal to zero. If a subject drops from the study before its end then his/her survival time is censored or missing, which is included in the dataset in order to avoid bias. Censoring can be left, right, or interval (refer Example 1). Dealing with censored/missing data is beyond the scope of this book. Replacing the missing data with zeroes, averages, or other values can significantly skew the results because the analysis will be based on a different sample that might not be representative of the population of interest. Each subject/machine survival prospects remain constant throughout the study period.
Observations are independent and each is only included once.
Moreover, because the dependent variable in survival analysis has two aspects: time to event and status, ordinary regression models cannot answer two important questions: Q1) whats the probability of surviving past a point in time (survival function)? Q2) whats the failure rate to a certain point in time (also known as hazard function)? E.g.; how many will die by the age of 75? How many years will the machine work properly before we need to buy a new one?
| Parametric | Non-parametric | Semi-parametric |
| Assume knowledge of the statistical distribution of survival times | Make no assumptions on the distribution of survival times like Kaplan Meier estimator | Has parametric and non-parametric components like the Cox regression model |
Median Mean 3rd Qu. Max. 59.0 368.0 476.0 599.5 794.8 1227.0 > summary(age) # subjects age Min. 1st Qu. Median Mean 3rd Qu. 38.89 50.17 56.85 56.17 62.38 74.50 > cor(futime, age) # pair-wise correlation [1] -0.6483612 > psymbol<-fustat+1 > table(psymbol) # 2 = censored psymbol 1 2 14 12 > plot(age, futime)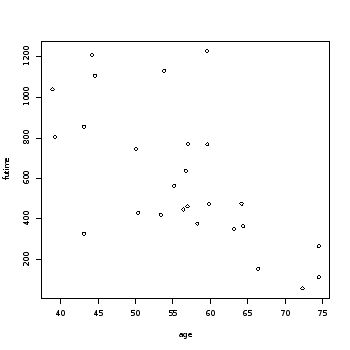 
plot(age, futime, pch=(psymbol))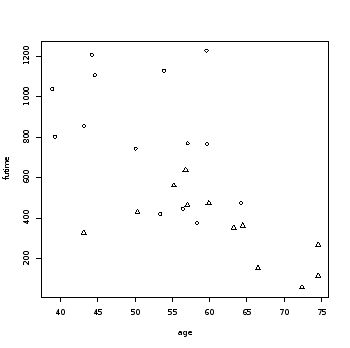 
> detach(ovarian)# so the variables do not overlap Interpretation: This dataset had 26 subjects (patients), and 12 censored observations (fustat). 38.89 50.17 56.85 56.17 62.38 74.50 > cor(futime, age) # pair-wise correlation [1] -0.6483612 > psymbol<-fustat+1 > table(psymbol) # 2 = censored psymbol 1 2 14 12 > plot(age, futime)
plot(age, futime, pch=(psymbol)) > detach(ovarian)# so the variables do not overlap Interpretation: This dataset had 26 subjects (patients), and 12 censored observations (fustat).
Survival time ranged from 59 to 1227 weeks, with an average of 599.8 weeks. The patients ages averaged at 56 years and ranged from 38.9 to 74.5 years. The first plot contrasts survival time against age regardless of censored status. Notice that as age increases survival time decreases. This is also manifested in the negative strong pairwise correlation between the two (-0.65) . The second plot differentiates the subjects with censored status (triangle = censored).
Censored ones are presented with triangles. They show relatively lower survival time.
Font size:
Interval:
Bookmark:
Similar books «Survival Analysis by Example: Hands on approach using R»
Look at similar books to Survival Analysis by Example: Hands on approach using R. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Survival Analysis by Example: Hands on approach using R and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.