1. Introduction and Motivation
Statistics is the science and art of making decisions based on quantitative evidence. This introductory chapter motivates the study of statistics by describing where and how it is used in all endeavors. It gives examples of applications, a little history of the subject, and a brief overview of the structure and content of the remaining chapters.
Almost all fields of study (including but not limited to physical science, social science, business, and economics) collect and interpret numerical data. Statistical techniques are the standard ways of summarizing and presenting the data, of turning data from an accumulation of numbers into usable information. Not all numbers are the same. No group of people are all the same height, no group has an identical income, not all cars get the same gas mileage, not all manufactured parts are absolutely identical. How much do they differ? Variability is the key concept that statistics offers. It is possible to measure how much things are not alike. We use standard deviation, variance, range, interquartile range, and MAD (median absolute deviation from the median) as measures of not-the-sameness. When we compare groups we compare their variability as well as their range.
Statistics uses many mathematical tools. The primary toolsalgebra, calculus, matrix algebra, analytic geometryare reviewed in Appendix I. Statistics is not purely mathematics. Mathematics problems are usually well specified and have a single correct answer on which all can agree. Data interpretation problems calling for statistics are not yet well specified. Part of the data analysts task is to specify the problem clearly enough that a mathematical tool may be used. Different answers to the same initial decision problem may be valid because a statistical analysis requires assumptions about the data and its manner of collection, and analysts can reasonably disagree about the plausibility of such assumptions.
Statistics uses many computational tools. In this book, we use R (R Core Team, ) as our primary tool for statistical analysis. R is an exceptionally well-developed tool for statistical research and analysis, that is for exploring and designing new techniques of analysis, as well as for analysis. We discuss installation and use of R in Appendix A.
We make liberal use of graphs in our presentations. Data analysts are responsible for the display of data with graphs and tables that summarize and represent the data and the analysis. Graphs are often the output of data analysis that provide the best means of communication between the data analyst and the client. We study a variety of display techniques.
While producing this book, we designed many innovative graphical displays of data and analyses. We introduce our displays in Section , we summarize the large class of newly created graphs that are based on Cartesian products.
The R code for all the graphs and tables in this book is included in the HH package for R (Heiberger, ). See Appendix B for a summary of the HH package. We consider the HH package to be an integral part of the book.
Statistics is an art. Skilled use of the mathematical tools is necessary but not sufficient. The data analyst must also know the subject area under study (or must work closely with a specialist in the subject area) to ensure an appropriate choice of statistical techniques for solving a problem. Experience, good judgment, and considerable creativity on the part of the statistical analyst are frequently needed.
Statistics is the science of doing science and is perhaps the only discipline that interfaces with all other sciences. Most statisticians have training or considerable knowledge in one or more areas other than statistics. The statistical analyst needs to communicate successfully both orally and in writing with the client for the analysis.
Statistics uses many communications skills, both written and oral. Results must be presented to the client and to the clients management. We discuss some of the mechanics of writing programs and technical reports in Appendices K, L, M, N, and O.
A common statistical problem is to discover the characteristics of an unobservable population by examining the corresponding characteristics of a sample randomly selected from the population and then (inductively) inferring the population characteristics (parameters) from the corresponding sample characteristics (statistics) . The task of selecting a random sample is not trivial. The discipline of statistics has developed a vast array of techniques for inferring from samples to populations, and for using probabilities to quantify the quality of such inferences.
Most statistical problems involve simultaneous consideration of several related measurements. Part of the statisticians task is to determine the interdependence among such measures, and then to account for it in the analysis.
The word statistics derives from the political science collections of numerical data describing demographics, business, politics that are useful for management of the state. The development of statistics as a scientific discipline dates from the end of the 19
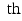
century with the design and analysis of agricultural experiments aimed at finding the best combination of fertilization, irrigation, and variety to maximize crop yield. Early in the 20
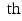
century, these ideas began to take hold in industry, with experiments designed to maximize output or minimize cost. Techniques for statistical analysis are developed in response to the needs of specific subject areas. Most of the techniques developed in one subject field can be applied unchanged to other subjects.
1.1 Statistics in Context
We write as if the statistician and the client are two separate people. In reality they are two separate roles and the same person often plays both roles. The client has a problem associated with the collection and interpretation of numerical data. The statistician is the expert in designing the data collection procedures and in calculating and displaying the results of statistical analyses.
The statisticians contribution to a research project typically includes the following steps:
Help the client phrase the question(s) to be answered in a manner that leads to sensible data collection and that is amenable to statistical analysis.
Design the experiment, survey, or other plan to approach the problem.
Gather the data.
Analyze the data.
Communicate the results.
In most statistics courses, including the one for which this book is designed, much of the time is spent learning how to perform step 4, the science of statistics. However, step 2, the art of statistics, is very important. If step 2 is poorly executed, the end results in step 5 will be misleading, disappointing, or useless. On the other hand, if step 4 is performed poorly following an excellent plan from step 2 and a correct execution of step 3, a reanalysis of the data (a new step 4) can save the day.
Today (2015) there are more than 18,000 statisticians practicing in the United States. Most fields in the biological, physical, and social sciences require training in statistics as educational background. Over 100 U.S. universities offer graduate degrees in statistics. Most firms of any size and most government agencies employ statisticians to assist in decision making. The profession of statistician is highly placed in the Jobs Rated Almanac Krantz ().
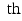 century with the design and analysis of agricultural experiments aimed at finding the best combination of fertilization, irrigation, and variety to maximize crop yield. Early in the 20
century with the design and analysis of agricultural experiments aimed at finding the best combination of fertilization, irrigation, and variety to maximize crop yield. Early in the 20  century, these ideas began to take hold in industry, with experiments designed to maximize output or minimize cost. Techniques for statistical analysis are developed in response to the needs of specific subject areas. Most of the techniques developed in one subject field can be applied unchanged to other subjects.
century, these ideas began to take hold in industry, with experiments designed to maximize output or minimize cost. Techniques for statistical analysis are developed in response to the needs of specific subject areas. Most of the techniques developed in one subject field can be applied unchanged to other subjects.