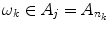Alexandr A. Borovkov Universitext Probability Theory 2013 10.1007/978-1-4471-5201-9_1 Springer-Verlag London 2013
1. Discrete Spaces of Elementary Events
1.1 Probability Space
To mathematically describe experiments with random outcomes, we will first of all need the notion of the space of elementary events (or outcomes ) corresponding to the experiment under consideration. We will denote by any set such that each result of the experiment we are interested in can be uniquely specified by the elements of .
In the simplest experiments we usually deal with finite spaces of elementary outcomes. In the coin tossing example we considered above, consists of two elements, heads and tails. In the die rolling experiment, the space is also finite and consists of 6 elements. However, even for tossing a coin (or rolling a die) one can arrange such experiments for which finite spaces of elementary events will not suffice. For instance, consider the following experiment: a coin is tossed until heads shows for the first time, and then the experiment is stopped. If t designates tails in a toss and h heads, then an elementary outcome of the experiment can be represented by a sequence ( tt th ). There are infinitely many such sequences, and all of them are different, so there is no way to describe unambiguously all the outcomes of the experiment by elements of a finite space.
Consider finite or countably infinite spaces of elementary events . These are the so-called discrete spaces. We will denote the elements of a space by the letter and call them elementary events (or elementary outcomes ).
The notion of the space of elementary events itself is mathematically undefinable: it is a primitive one, like the notion of a point in geometry. The specific nature of will, as a rule, be of no interest to us.
Any subset A will be called an event (the event A occurs if any of the elementary outcomes A occurs).
The union or sum of two events A and B is the event A B (which may also be denoted by A + B ) consisting of the elementary outcomes which belong to at least one of the events A and B . The product or intersection AB (which is often denoted by A B as well) is the event consisting of all elementary events belonging to both A and B . The difference of the events A and B is the set A B (also often denoted by A B ) consisting of all elements of A not belonging to B . The set is called the certain event. The empty set is called the impossible event. The set
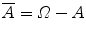
is called the complementary event of A . Two events A and B are mutually exclusive if AB =.
Let, for instance, our experiment consist in rolling a die twice. Here one can take the space of elementary events to be the set consisting of 36 elements ( i , j ), where i and j run from 1 to 6 and denote the numbers of points that show up in the first and second roll respectively. The events A ={ i + j 3} and B ={ j =6} are mutually exclusive. The product of the events A and C ={ j is even} is the event (1,2). Note that if we were interested in the events related to the first roll only, we could consider a smaller space of elementary events consisting of just 6 elements i =1,2,,6.
One says that the probabilities of elementary events are given if a nonnegative real-valued function P is given on such that P ()=1 (one also says that the function P specifies a probability distribution on ).
The probability of an event A is the number
This definition is consistent, for the series on the right hand side is absolutely convergent.
We note here that specific numerical values of the function P will also be of no interest to us: this is just an issue of the practical value of the model. For instance, it is clear that, in the case of a symmetric die, for the outcomes 1,2,,6 one should put P (1)= P (2)== P (6)=1/6; for a symmetric coin, one has to choose the values P ( h )= P ( t )=1/2 and not any others. In the experiment of tossing a coin until heads shows for the first time, one should put P ( h )=1/2, P ( th )=1/22, P ( tth )=1/23,. Since
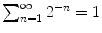
, the function P given in this way on the outcomes of the form ( t th ) will define a probability distribution on . For example, to calculate the probability that the experiment stops on an even step (that is, the probability of the event composed of the outcomes ( th ),( ttth ),), one should consider the sum of the corresponding probabilities which is equal to
In the experiments mentioned in the Introduction, where one had to guess when a device will break downbefore a given time (the event A ) or after it, quantitative estimates of the probability P ( A ) can usually only be based on the results of the experiments themselves. The methods of estimating unknown probabilities from observation results are studied in Mathematical Statistics, the subject-matter of which will be exemplified somewhat later by a problem from this chapter.
Note further that by no means can one construct models with discrete spaces of elementary events for all experiments. For example, suppose that one is measuring the energy of particles whose possible values fill the interval [0, V ], V >0, but the set of points of this interval (that is, the set of elementary events) is continuous. Or suppose that the result of an experiment is a patients electrocardiogram. In this case, the result of the experiment is an element of some functional space. In such cases, more general schemes are needed.
From the above definitions, making use of the absolute convergence of the series A P (), one can easily derive the following properties of probability:
(2)
P ( A + B )= A B P ()= A P ()+ B P () A B P ()= P ( A )+ P ( B ) P ( AB ).
(3)
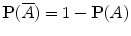
.
This entails, in particular, that, for disjoint (mutually exclusive) events A and B ,
This property of the additivity of probability continues to hold for an arbitrary number of disjoint events A 1, A 2,: if A i A j = for i j , then
This follows from the equality
and the fact that
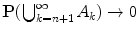
as n . To prove the last relation, first enumerate the elementary events. Then we will be dealing with the sequence 1, 2,; k =, P ( k > n k )= k > n P ( k )0 as n . Denote by n k the number of events A j such that
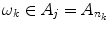
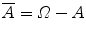 is called the complementary event of A . Two events A and B are mutually exclusive if AB =.
is called the complementary event of A . Two events A and B are mutually exclusive if AB =.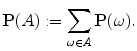
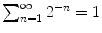 , the function P given in this way on the outcomes of the form ( t th ) will define a probability distribution on . For example, to calculate the probability that the experiment stops on an even step (that is, the probability of the event composed of the outcomes ( th ),( ttth ),), one should consider the sum of the corresponding probabilities which is equal to
, the function P given in this way on the outcomes of the form ( t th ) will define a probability distribution on . For example, to calculate the probability that the experiment stops on an even step (that is, the probability of the event composed of the outcomes ( th ),( ttth ),), one should consider the sum of the corresponding probabilities which is equal to 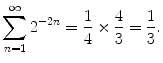
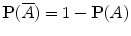 .
.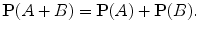
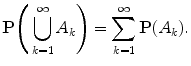
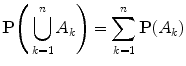
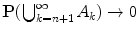 as n . To prove the last relation, first enumerate the elementary events. Then we will be dealing with the sequence 1, 2,; k =, P ( k > n k )= k > n P ( k )0 as n . Denote by n k the number of events A j such that
as n . To prove the last relation, first enumerate the elementary events. Then we will be dealing with the sequence 1, 2,; k =, P ( k > n k )= k > n P ( k )0 as n . Denote by n k the number of events A j such that