PROBABILITY
THEORYA CONCISE COURSEPROBABILITY
THEORYA CONCISE COURSEY.A.ROZANOVRevised English EditionTranslated and Edited by Richard A. Silverman DOVER PUBLICATIONS, INC. NEW YORK Copyright 1969 by Richard A. Silverman.
All rights reserved. This Dover edition, first published in 1977, is an unabridged and slightly corrected republication of the revised English edition published by Prentice-Hall Inc., Englewood Cliffs, N. International Standard Book Number: 0-486-63544-9Library of Congress Catalog Card Number: 77-78592 Manufactured in the United States by Courier Corporation 63544916 www.doverpublications.com EDITORS PREFACE This book is a concise introduction to modern probability theory and certain of its ramifications. International Standard Book Number: 0-486-63544-9Library of Congress Catalog Card Number: 77-78592 Manufactured in the United States by Courier Corporation 63544916 www.doverpublications.com EDITORS PREFACE This book is a concise introduction to modern probability theory and certain of its ramifications.
By deliberate succinctness of style and judicious selection of topics, it manages to be both fast-moving and self-contained. The present edition differs from the Russian original (Moscow, 1968) in several respects: 1. It has been heavily restyled with the addition of some new material. Here I have drawn from my own background in probability theory, information theory, etc. 2. Each of the eight chapters and four appendices has been equipped with relevant problems, many accompanied by hints and answers.
There are 150 of these problems, in large measure drawn from the excellent collection edited by A. A. Sveshnikov (Moscow, 1965). 3. At the end of the book I have added a brief Bibliography, containing suggestions for collateral and supplementary reading. A. S. BASIC CONCEPTS1. BASIC CONCEPTS1.
Probability and Relative Frequency Consider the simple experiment of tossing an unbiased coin. This experiment has two mutually exclusive outcomes, namely heads and tails. The various factors influencing the outcome of the experiment are too numerous to take into account, at least if the coin tossing is fair. Therefore the outcome of the experiment is said to be random. Everyone would certainly agree that the probability of getting heads and the probability of getting tails both equal 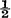 . Intuitively, this answer is based on the idea that the two outcomes are equally likely or equiprobable, because of the very nature of the experiment.
. Intuitively, this answer is based on the idea that the two outcomes are equally likely or equiprobable, because of the very nature of the experiment.
But hardly anyone will bother at this point to clarify just what he means by probability. Continuing in this vein and taking these ideas at face value, consider an experiment with a finite number of mutually exclusive outcomes which are equiprobable, i.e., equally likely because of the nature of the experiment. Let A denote some event associated with the possible outcomes of the experiment. Then the probability P(A) of the event A is defined as the fraction of the outcomes in which A occurs. More exactly,  where N is the total number of outcomes of the experiment and N(A) is the number of outcomes leading to the occurrence of the event A. Example 1. In tossing a well-balanced coin, there are N = 2 mutually exclusive equiprobable outcomes (heads and tails).
where N is the total number of outcomes of the experiment and N(A) is the number of outcomes leading to the occurrence of the event A. Example 1. In tossing a well-balanced coin, there are N = 2 mutually exclusive equiprobable outcomes (heads and tails).
Let A be either of these two outcomes. Then N(A) = 1, and hence 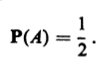 Example 2. In throwing a single unbiased die, there are N = 6 mutually exclusive equiprobable outcomes, namely getting a number of spots equal to each of the numbers 1 through 6. Let A be the event consisting of getting an even number of spots. Then there are N(A) = 3 outcomes leading to the occurrence of A (which ones?), and hence
Example 2. In throwing a single unbiased die, there are N = 6 mutually exclusive equiprobable outcomes, namely getting a number of spots equal to each of the numbers 1 through 6. Let A be the event consisting of getting an even number of spots. Then there are N(A) = 3 outcomes leading to the occurrence of A (which ones?), and hence 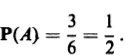 Example 3. In throwing a pair of dice, there are N = 36 mutually exclusive equiprobable events, each represented by an ordered pair (a, b), where a is the number of spots showing on the first die and b the number showing on the second die. Let A be the event that both dice show the same number of spots. Then A occurs whenever a = b, i.e., n(A) = 6.
Example 3. In throwing a pair of dice, there are N = 36 mutually exclusive equiprobable events, each represented by an ordered pair (a, b), where a is the number of spots showing on the first die and b the number showing on the second die. Let A be the event that both dice show the same number of spots. Then A occurs whenever a = b, i.e., n(A) = 6.
Therefore 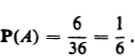 Remark. Despite its seeming simplicity, formula () in a given problem, we must find all the equiprobable outcomes, and then identify all those leading to the occurrence of the event A in question. The accumulated experience of innumerable observations reveals a remarkable regularity of behavior, allowing us to assign a precise meaning to the concept of probability not only in the case of experiments with equiprobable outcomes, but also in the most general case. Suppose the experiment under consideration can be repeated any number of times, so that, in principle at least, we can produce a whole series of independent trials under identical conditions, in each of which, depending on chance, a particular event A of interest either occurs or does not occur. Let n be the total number of experiments in the whole series of trials, and let n(A) be the number of experiments in which A occurs. Then the ratio
Remark. Despite its seeming simplicity, formula () in a given problem, we must find all the equiprobable outcomes, and then identify all those leading to the occurrence of the event A in question. The accumulated experience of innumerable observations reveals a remarkable regularity of behavior, allowing us to assign a precise meaning to the concept of probability not only in the case of experiments with equiprobable outcomes, but also in the most general case. Suppose the experiment under consideration can be repeated any number of times, so that, in principle at least, we can produce a whole series of independent trials under identical conditions, in each of which, depending on chance, a particular event A of interest either occurs or does not occur. Let n be the total number of experiments in the whole series of trials, and let n(A) be the number of experiments in which A occurs. Then the ratio 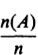 is called the relative frequency of the event A (in the given series of trials). It turns out that the relative frequencies n(A)/n observed in different series of trials are virtually the same for large n, clustering about some constant
is called the relative frequency of the event A (in the given series of trials). It turns out that the relative frequencies n(A)/n observed in different series of trials are virtually the same for large n, clustering about some constant  called the probability of the event A.
called the probability of the event A.
More exactly, () means that  Roughly speaking, the probability P(A) of the event A equals the fraction of experiments leading to the occurrence of A in a large series of trials. Example 4. . Note that the relative frequency of occurrence of heads is even closer to
Roughly speaking, the probability P(A) of the event A equals the fraction of experiments leading to the occurrence of A in a large series of trials. Example 4. . Note that the relative frequency of occurrence of heads is even closer to 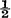 if we group the tosses in series of 1000 tosses each. Table 1. Number of heads in a series of coin tosses
if we group the tosses in series of 1000 tosses each. Table 1. Number of heads in a series of coin tosses 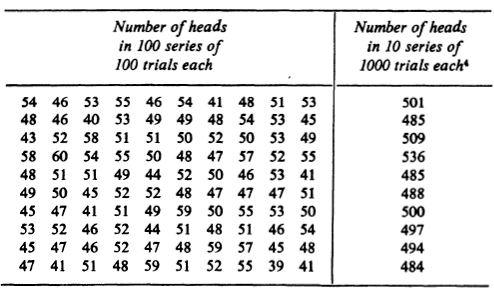 Example 5 (De Mrs paradox). As a result of extensive observation of dice games, the French gambler de Mr noticed that the total number of spots showing on three dice thrown simultaneously turns out to be 11 (the event
Example 5 (De Mrs paradox). As a result of extensive observation of dice games, the French gambler de Mr noticed that the total number of spots showing on three dice thrown simultaneously turns out to be 11 (the event
Next page













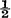 . Intuitively, this answer is based on the idea that the two outcomes are equally likely or equiprobable, because of the very nature of the experiment.
. Intuitively, this answer is based on the idea that the two outcomes are equally likely or equiprobable, because of the very nature of the experiment. where N is the total number of outcomes of the experiment and N(A) is the number of outcomes leading to the occurrence of the event A. Example 1. In tossing a well-balanced coin, there are N = 2 mutually exclusive equiprobable outcomes (heads and tails).
where N is the total number of outcomes of the experiment and N(A) is the number of outcomes leading to the occurrence of the event A. Example 1. In tossing a well-balanced coin, there are N = 2 mutually exclusive equiprobable outcomes (heads and tails).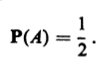 Example 2. In throwing a single unbiased die, there are N = 6 mutually exclusive equiprobable outcomes, namely getting a number of spots equal to each of the numbers 1 through 6. Let A be the event consisting of getting an even number of spots. Then there are N(A) = 3 outcomes leading to the occurrence of A (which ones?), and hence
Example 2. In throwing a single unbiased die, there are N = 6 mutually exclusive equiprobable outcomes, namely getting a number of spots equal to each of the numbers 1 through 6. Let A be the event consisting of getting an even number of spots. Then there are N(A) = 3 outcomes leading to the occurrence of A (which ones?), and hence 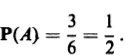 Example 3. In throwing a pair of dice, there are N = 36 mutually exclusive equiprobable events, each represented by an ordered pair (a, b), where a is the number of spots showing on the first die and b the number showing on the second die. Let A be the event that both dice show the same number of spots. Then A occurs whenever a = b, i.e., n(A) = 6.
Example 3. In throwing a pair of dice, there are N = 36 mutually exclusive equiprobable events, each represented by an ordered pair (a, b), where a is the number of spots showing on the first die and b the number showing on the second die. Let A be the event that both dice show the same number of spots. Then A occurs whenever a = b, i.e., n(A) = 6.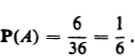 Remark. Despite its seeming simplicity, formula () in a given problem, we must find all the equiprobable outcomes, and then identify all those leading to the occurrence of the event A in question. The accumulated experience of innumerable observations reveals a remarkable regularity of behavior, allowing us to assign a precise meaning to the concept of probability not only in the case of experiments with equiprobable outcomes, but also in the most general case. Suppose the experiment under consideration can be repeated any number of times, so that, in principle at least, we can produce a whole series of independent trials under identical conditions, in each of which, depending on chance, a particular event A of interest either occurs or does not occur. Let n be the total number of experiments in the whole series of trials, and let n(A) be the number of experiments in which A occurs. Then the ratio
Remark. Despite its seeming simplicity, formula () in a given problem, we must find all the equiprobable outcomes, and then identify all those leading to the occurrence of the event A in question. The accumulated experience of innumerable observations reveals a remarkable regularity of behavior, allowing us to assign a precise meaning to the concept of probability not only in the case of experiments with equiprobable outcomes, but also in the most general case. Suppose the experiment under consideration can be repeated any number of times, so that, in principle at least, we can produce a whole series of independent trials under identical conditions, in each of which, depending on chance, a particular event A of interest either occurs or does not occur. Let n be the total number of experiments in the whole series of trials, and let n(A) be the number of experiments in which A occurs. Then the ratio 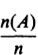 is called the relative frequency of the event A (in the given series of trials). It turns out that the relative frequencies n(A)/n observed in different series of trials are virtually the same for large n, clustering about some constant
is called the relative frequency of the event A (in the given series of trials). It turns out that the relative frequencies n(A)/n observed in different series of trials are virtually the same for large n, clustering about some constant  called the probability of the event A.
called the probability of the event A. Roughly speaking, the probability P(A) of the event A equals the fraction of experiments leading to the occurrence of A in a large series of trials. Example 4. . Note that the relative frequency of occurrence of heads is even closer to
Roughly speaking, the probability P(A) of the event A equals the fraction of experiments leading to the occurrence of A in a large series of trials. Example 4. . Note that the relative frequency of occurrence of heads is even closer to  Example 5 (De Mrs paradox). As a result of extensive observation of dice games, the French gambler de Mr noticed that the total number of spots showing on three dice thrown simultaneously turns out to be 11 (the event
Example 5 (De Mrs paradox). As a result of extensive observation of dice games, the French gambler de Mr noticed that the total number of spots showing on three dice thrown simultaneously turns out to be 11 (the event