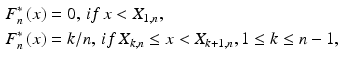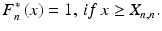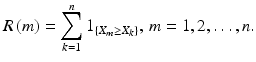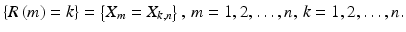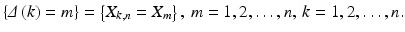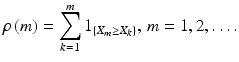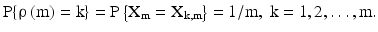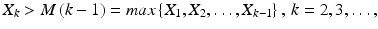1. Introduction
Let x 1 , x 2, , x n denote results of n participants, which were registered in some sport competition. These values can be presented in the increasing order as x 1, n x 2, n x n 1, n x n , n , where x 1, n = min{ x 1, x 2, , x n } and x n , n = max{ x 1, x 2, , x n }. In some competitions (take, for example, any running distance) x 1, n , x 2, n and x 3 ,n are correspondingly the results of the gold, silver and bronze prizewinners. For other type of competitions (say, for high jumping or long jumping) x n , n , x n 1, n and x n 2, n are the best results. Indeed, after finishing this competition we deal with some concrete values x 1 , x 2, , x n and x 1, n , x 2 ,n , , x n , n . Before the competition, the future results of the participants are unknown to us, and we can consider these results as random values X 1 , X 2, , X n . Indeed, values X 1, n = min{ X 1, X 2, , X n } and X n , n = max{ X 1, X 2, , X n }, as well as other ordered values X 2, n X n 1, n , are random. Up to the beginning of the competition all sport newspapers will discuss the probable realizations of random values X 1, n X n,n and the chances of a particular participant to become the winner, i.e. his/her chances to reach the result X 1, n (or X n , n ).
This simple example shows the necessity of knowing how to work with the so-called order statistics X 1, n X n,n and their realizations x 1 ,n x n , n .
Below some definitions connected with order statistics are given.
Let X 1 , X 2, , X n be initial random variables. The set of the observed values { x 1, x 2, , x n } of random variables X 1, X 2, , X n is called a realization of these X s. In the most part of the book we suppose that X 1 , X 2,, X n are independent identically distributed (i.i.d.) random variables, or simply we can say in this situation that X 1, X 2, , X n present n independent observations on X where X is a random variable having a certain distribution function (d.f.) F .
Then the combination X 1, n X 2, n X n , n denotes the variational series based on random variables X 1, X 2, , X n . If X s are independent and identically distributed one can say that X 1, n X 2 , n X n,n is the variational series based on a sample X 1, X 2 ,, X n .
Elements X k , n , 1 k n, are called order statistics ( order statistics based on a sample X 1, X 2, , X n ; order statistics from d.f. F; ordered observations on X ) . We denote the observed values of X 1 ,n , X 2, n , , X n , n as above, x 1, n , x 2 ,n , , x n , n , and call them realizations of order statistics. Let us note that X 1, n = m ( n ) = min{ X 1, X 2, , X n } and X n , n = M ( n ) = max{ X 1, X 2, , X n }, n = 1, 2 , . Rather natural is the following equality :
Together with the sample X 1, X 2, , X n it is naturally to consider the empirical ( or sample ) distribution function
Here
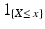
is a random indicator, which equals to 1 if X x and to 0 if X > x.
Let us mention that
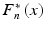
can be expressed in terms of order statistics X k , n as follows:
and
Usually a random sample X 1 , X 2, , X n is accompanied by the corresponding vector of ranks ( R (1), R (2), , R ( n )) , where
These ranks provide the following equalities for events:
Together with ranks we can use the so - called antiranks (1) , (2), , ( n ) , which are defined by equalities
One more type of ranks is presented by sequential ranks. For any sequence of random variables X 1, X 2, we introduce sequential ranks (1) , (2), as follows :
Sequential rank (m) shows the position of a new coming observation X m among its predecessors X 1, X 2, , X m 1. If independent random variables X 1, X 2, , X m have the same continuous distribution then it is possible to see that for any m = 1, 2,
Here we use the fact that if X s are independent and have continuous distributions then any two of them can coincide with zero probability and the situation of symmetry, which provides that all m events { X m = X 1, m }, , { X m = X m , m } have the same probability.
The more complicate theory of order statistics and all types of ranks can be found in Ahsanullah and Nevzorov (2001a, 2005), Ahsanullah, Nevzorov and Shakil (2013), Arnold and Balakrishnan (1989). In Chap. we will present some results for order statistics, which our reader will recall working with record times and record values.
Now let us come back to the results of the participants of some sport distance (say, 100 m running). Each year hundreds of competitions are organized, in which thousands of sportsmen run 100 m. Even the most serious lover of the field athletics cannot get and investigate all the results. Indeed, it is possible to operate with the results of participants of the Olympic Games and World championships but it is impossible to have information about participants of all these competitions.
Meantime there are the most interesting results, which can be easily found in a number of sport editionsworld records, records of Olympic Games, continental and countries record values. Indeed, sport records are very popular, but record values in any domain of human activities are also interesting for millions of citizens worldwide.
Let us come back to the sequence of random variables X 1 , X 2, . There are two classical types of record valuesupper and lower records. We say that X k is the upper record value if














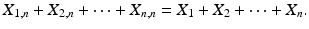
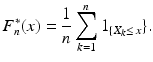
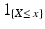 is a random indicator, which equals to 1 if X x and to 0 if X > x.
is a random indicator, which equals to 1 if X x and to 0 if X > x.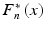 can be expressed in terms of order statistics X k , n as follows:
can be expressed in terms of order statistics X k , n as follows: