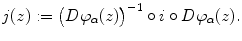The purpose of this chapter is to provide the material necessary for understanding convergence of Riemann surfaces in the sense of DeligneMumford. If we want to discuss the convergence behavior of a sequence of J -holomorphic curves ( u k ) we need to take into account that their domains are all different Riemann surfaces ( S , j k ). The aim is to establish a suitable notion of convergence for these as well. The discussion here follows Thurstons approach [] as general references). The details, however, are spread out over the literature so we give a thorough and unified presentation.
1.1 Smooth and Noded Riemann Surfaces
Definition 1.1
An atlas on a smooth surface S with charts
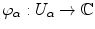
, U = S is called conformal if the transition maps
are holomorphic. A conformal structure on S is a maximal conformal atlas. A smooth surface S together with a conformal structure is called a Riemann surface . A continuous map f : S S between two Riemann surfaces is called holomorphic if in local coordinates { U , } on S and
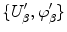
on S the maps
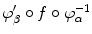
are holomorphic whenever they are defined. A holomorphic map f : S S is called conformal if its derivative is never zero.
It is common practice to identify a coordinate patch U S with its image
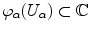
suppressing the coordinate map in the notation. This makes sense if we consider local objects and notions which are invariant under conformal maps. For example, if
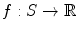
is a smooth function on a Riemann surface then we may define f is subharmonic by the requirement that
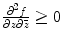
. This is well-defined if for any locally defined conformal map z = h ( w ) the map f h satisfies
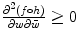
. But this follows from
From this it is clear that the local expression
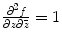
for example would not make sense globally on a Riemann surface. The following statements hold (the proofs are trivial and we leave them to the reader):
(1)
Every Riemann surface is orientable.
(2)
Assume S is a Riemann surface, S is a smooth surface and : S S is a local diffeomorphism. Then there exists a unique conformal structure on S such that becomes holomorphic.
(3)
Application: Every covering space of a Riemann surface can be made into a Riemann surface in a canonical fashion.
(4)
Let S be a Riemann surface, let S be a smooth surface and let : S S be a covering. If every covering transformation : S S is holomorphic then there is a unique conformal structure on S such that becomes holomorphic.
There are different ways to look at Riemann surfaces. We will elaborate on some of them and explain why they are equivalent to Definition 1.1.
Definition 1.2
(Almost complex structure-Alternative definition of Riemann surface)
Let W be a differentiable manifold. An almost complex structure on M is a smooth section j of the vector bundle
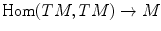
,
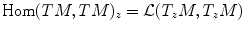
such that
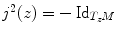
for all z M . A pair ( S , j ) consisting of a smooth surface S and an almost complex structure j is called a Riemann surface .
The two notions of Riemann surface are equivalent: Assume S is a smooth surface together with a conformal structure. Then we can define an almost complex structure j on S as follows: Let z S . Let
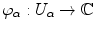
be a coordinate chart belonging to the conformal structure. We define
Show as an exercise that this definition does not depend on the choice of the coordinate chart . This procedure also works for general complex manifolds, i.e. smooth manifolds of even dimension which admit an atlas with holomorphic coordinate transition maps. The converse procedure would be constructing a conformal structure on a manifold with a given almost complex structure j such that () holds.
Definition 1.3
Assume that W is a manifold with an almost complex structure j . If W admits an atlas such that the transition maps between coordinate patches are all holomorphic, and if j is then given by () then it is called a complex structure or an integrable almost complex structure .
Remark 1.4
The existence question of an almost complex structure on a given even dimensional manifold M is rather a topological question while the existence question of an integrable almost complex structure is of analytical nature, and it is usually more difficult to answer. For example, it is known that the only spheres admitting almost complex structures are S 2 and S 6. By our remarks above every almost complex structure on S 2 is integrable. On the other hand, it is an open question whether S 6 admits any complex structure.















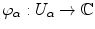 , U = S is called conformal if the transition maps
, U = S is called conformal if the transition maps 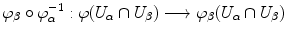
 on S the maps
on S the maps 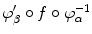 are holomorphic whenever they are defined. A holomorphic map f : S S is called conformal if its derivative is never zero.
are holomorphic whenever they are defined. A holomorphic map f : S S is called conformal if its derivative is never zero.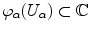 suppressing the coordinate map in the notation. This makes sense if we consider local objects and notions which are invariant under conformal maps. For example, if
suppressing the coordinate map in the notation. This makes sense if we consider local objects and notions which are invariant under conformal maps. For example, if 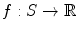 is a smooth function on a Riemann surface then we may define f is subharmonic by the requirement that
is a smooth function on a Riemann surface then we may define f is subharmonic by the requirement that 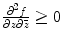 . This is well-defined if for any locally defined conformal map z = h ( w ) the map f h satisfies
. This is well-defined if for any locally defined conformal map z = h ( w ) the map f h satisfies 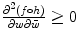 . But this follows from
. But this follows from 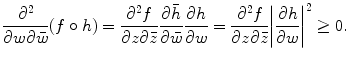
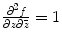 for example would not make sense globally on a Riemann surface. The following statements hold (the proofs are trivial and we leave them to the reader):
for example would not make sense globally on a Riemann surface. The following statements hold (the proofs are trivial and we leave them to the reader): 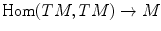 ,
, 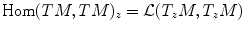 such that
such that 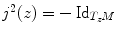 for all z M . A pair ( S , j ) consisting of a smooth surface S and an almost complex structure j is called a Riemann surface .
for all z M . A pair ( S , j ) consisting of a smooth surface S and an almost complex structure j is called a Riemann surface .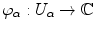 be a coordinate chart belonging to the conformal structure. We define
be a coordinate chart belonging to the conformal structure. We define