Ayres Frank - Schaums outlines of calculus

The late FRANK AYRES, Jr., PhD, was formerly professor and head of the Department at Dickinson College, Carlisle, Pennsylvania. He is the author of eight Schaums Outlines, including Calculus, Differential Equations, 1st Year College Math, and Matrices.Elliott Mendelson, PhD, is professor of mathematics at Queens College. He is the author of Schaums Outline of Beginning Calculus. Copyright 2013 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN: 978-0-07-179554-8
MHID: 0-07-179554-5 The material in this eBook also appears in the print version of this title: ISBN: 978-0-07-179553-1, MHID: 0-07-179553-7.

All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. To contact a representative please e-mail us at bulksales@mcgraw-hill.com. McGraw-Hill, the McGraw-Hill Publishing logo, Schaums, and related trade dress are trademarks or registered trademarks of The McGraw-Hill Companies and/or its affiliates in the United States and other countries and may not be used without written permission.

All other trademarks are the property of their respective owners. The McGraw-Hill Companies is not associated with any product or vendor mentioned in this book. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (McGraw-Hill) and its licensors reserve all rights in and to the work. Use of this work is subject to these terms. Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work, you may not decompile, disassemble, reverse engineer, reproduce, modify, create derivative works based upon, transmit, distribute, disseminate, sell, publish or sublicense the work or any part of it without McGraw-Hills prior consent.

You may use the work for your own noncommercial and personal use; any other use of the work is strictly prohibited. Your right to use the work may be terminated if you fail to comply with these terms. THE WORK IS PROVIDED AS IS. McGRAW-HILL AND ITS LICENSORS MAKE NO GUARANTEES OR WARRANTIES AS TO THE ACCURACY, ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE, AND EXPRESSLY DISCLAIM ANY WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. McGraw-Hill and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free. Neither McGraw-Hill nor its licensors shall be liable to you or anyone else for any inaccuracy, error or omission, regardless of cause, in the work or for any damages resulting therefrom.

McGraw-Hill has no responsibility for the content of any information accessed through the work. Under no circumstances shall McGraw-Hill and/or its licensors be liable for any indirect, incidental, special, punitive, consequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.

The purpose of this book is to help students understand and use the calculus. Everything has been aimed toward making this easier, especially for students with limited background in mathematics or for readers who have forgotten their earlier training in mathematics. The topics covered include all the material of standard courses in elementary and intermediate calculus.

The direct and concise exposition typical of the Schaum Outline series has been amplified by a large number of examples, followed by many carefully solved problems. In choosing these problems, we have attempted to anticipate the difficulties that normally beset the beginner. In addition, each chapter concludes with a collection of supplementary exercises with answers. This sixth edition has enlarged the number of solved problems and supplementary exercises. Moreover, we have made a great effort to go over ticklish points of algebra or geometry that are likely to confuse the student. The author believes that most of the mistakes that students make in a calculus course are not due to a deficient comprehension of the principles of calculus, but rather to their weakness in high-school algebra or geometry.

Students are urged to continue the study of each chapter until they are confident about their mastery of the material. A good test of that accomplishment would be their ability to answer the supplementary problems. The author would like to thank many people who have written to me with corrections and suggestions, in particular Danielle Cinq-Mars, Lawrence Collins, L.D. De Jonge, Konrad Duch, Stephanie Happ, Lindsey Oh, and Stephen B. Soffer. He is also grateful to his editor, Charles Wall, for all his patient help and guidance.

ELLIOTT MENDELSON

A linear coordinate system is a graphical representation of the real numbers as the points of a straight line. To each number corresponds one and only one point, and to each point corresponds one and only one number. To set up a linear coordinate system on a given line: (1) select any point of the line as the origin and let that point correspond to the number 0; (2) choose a positive direction on the line and indicate that direction by an arrow; (3) choose a fixed distance as a unit of measure. If x is a positive number, find the point corresponding to x by moving a distance of x units from the origin in the positive direction.

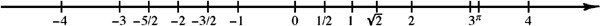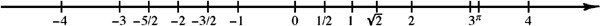If x is negative, find the point corresponding to x by moving a distance of x units from the origin in the negative direction. (For example, if x = 2, then x = 2 and the corresponding point lies 2 units from the origin in the negative direction.) See . Fig. 11 The number assigned to a point by a coordinate system is called the coordinate of that point. We often will talk as if there is no distinction between a point and its coordinate. Thus, we might refer to the point 3 rather than to the point with coordinate 3.