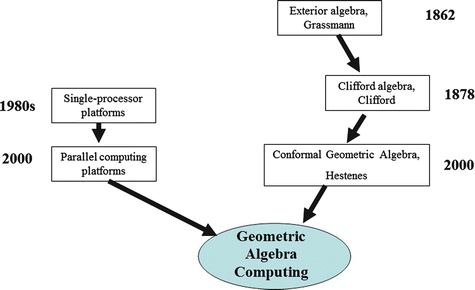
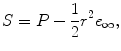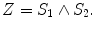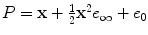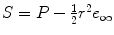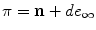What mathematicians often call Clifford algebra may also be called Geometric Algebra if the focus is on the geometric meaning of the algebraic expressions and operators. Geometric Algebra is a mathematical framework that makes it easy to describe geometric concepts and operations. It allows us to develop algorithms fast and in an intuitive way.
In this chapter we highlight some benefits and present the history of Geometric Algebra Computing. At the end of the chapter, we give an outline of the structure of this book.
1.1 The Benefits of Geometric Algebra
We focus especially in this book on Conformal Geometric Algebra (CGA). In the following, we highlight some of its properties, that make it advantageous for many engineering applications, namely
Unification of many mathematical systems in one easy-to-understand mathematical system;
Intuitive handling of geometric objects;
Intuitive handling of geometric operations.
In the wide range of engineering applications, many different mathematical systems are currently used. One notable advantage of Geometric Algebra is that it subsumes mathematical systems such as vector algebra, complex numbers, quaternions, and Plcker coordinates. Table , for instance, describes how complex numbers can be identified in 2D Geometric Algebra. This algebra contains not only the two basis vectors e 1 and e 2, but also basis elements of grade (dimension) 0 and 2. Grade 0 represents scalars. With the help of the rules of Geometric Algebra, it can be shown quite easily that the element e 1 e 2 (of grade 2) squares to1 and can be identified with the imaginary unit i . Linear combinations of these two elements describe all complex numbers.
Table 1.1
Multiplication table of 2D Geometric Algebra. This algebra consists of basic algebraic objects of grade (dimension) 0, the scalar, of grade 1, the two basis vectors e 1 and e 2 and of grade 2, the bivector e 1 e 2, which can be identified with the imaginary number i squaring to1
| | e 1 | e 2 | e 1 e 2 |
|---|
| | e 1 | e 2 | e 1 e 2 |
e 1 | e 1 | | e 1 e 2 | e 2 |
e 2 | e 2 | e 1 e 2 | | e 1 |
e 1 e 2 | e 1 e 2 | e 2 | e 1 | |
The imaginary unit i can be also identified as the element e 1 e 2 in Conformal Geometric Algebra as indicated in Fig..
Fig. 1.2
The blades of CGA. Spheres and planes, for instance, are vectors. Lines and circles can be represented as bivectors. Other mathematical systems such as complex numbers and quaternions can be identified based on their imaginary units i , j , k . This is why transformations such as rotations can also be handled in the algebra
Conformal Geometric Algebra, considered as a 5D Geometric Algebra, is based on the 3D basis vectors e 1, e 2 and e 3 and on two additional basis vectors e 0, representing the origin, and e , representing infinity. Looking more into the details of Conformal Geometric Algebra, it consists of blades with grades (dimension) 0, 1, 2, 3, 4 and 5, where a scalar is a 0-blade (a blade of grade 0). The element of grade 5 is called the pseudoscalar. A linear combination of k-blades is called a k-vector . So, a bivector is a linear combination of blades with grade 2. Other k-vectors are vectors (grade 1), bivectors (grade 2), trivectors (grade 3), and quadvectors (grade 4). A linear combination of blades of different grades is called a multivector . Multivectors are the general elements of Geometric Algebra. Figure lists all 32 blades of Conformal Geometric Algebra.
This algebra is able to treat several different types of geometric objects, easily. Table , for instance. These spheres are represented simply by
based on their center point P , their radius r , and the basis vector e . The circle of intersection of two spheres is then easily computed by using the outer product to operate on the spheres, as simply as if they were vectors:
Many applications in computer graphics, computer vision, and other areas of engineering can benefit from these properties. In a ray-tracing application, for instance, the intersection of a ray and a bounding sphere can easily be expressed with the help of the outer product of these two geometric entities (Fig.).
Table 1.2
List of the basic geometric primitives provided by 5D Conformal Geometric Algebra. The bold characters represent 3D entities ( x is a 3D point, n is a 3D normal vector, and x 2 is a scalar product of the 3D vector x ). The two additional basis vectors e 0 and e represent the origin and infinity. Based on the outer product, circles and lines can be described as intersections of two spheres and of two planes, respectively. The parameter r represents the radius of the sphere, and the parameter d the distance from the origin to the plane
Entity | Representation |
|---|
Point | |
Sphere | |
Plane | |
Circle | Z = S 1 S 2 |
Line | L =12 |











![Dietmar Hamann [Dietmar Hamann] - The Didi Man](/uploads/posts/book/46092/thumbs/dietmar-hamann-dietmar-hamann-the-didi-man.jpg)