Dietmar Hildenbrand - Introduction to Geometric Algebra Computing; First Edition

Dietmar Hildenbrands new book Introduction to Geometric Algebra Computingin my view fills an important gap in Cliffords geometric algebra literature. Most books up till now are written for the level of college students or above, pre-supposing substantial levels of linear-, vector- and matrix algebra, complex numbers, calculus, etc. The current book though starts with the elementary two-dimensional Euclidean geometry as I remember it from my middle school days. Therefore I expect that this book can be of interest beginning at the middle school level, through high school and college education. Furthermore engineers, who look for a beginners introduction to geometric algebra are also at the right address. Because the textbook pedagogically begins by defining all geometric objects, the measuring of distance and angle, and elementary geometric transformations, after having shown how to work interactively on the universal (can be implemented on all computing platforms) GAALOPScript. The latter permits the reader to immediately try and vary every new item, definition, entity, computation, etc. This is greatly assisted by the extensive set of GAALOPScript listings. In this sense the textbook is fully (inter)activ; the reader does not have to persevere through extensive theoretical foundations, before reaching the first motivating application, or explorative problem. At his own pace the reader can try the listed code of a section, and study the accompanying text for deeper understanding.

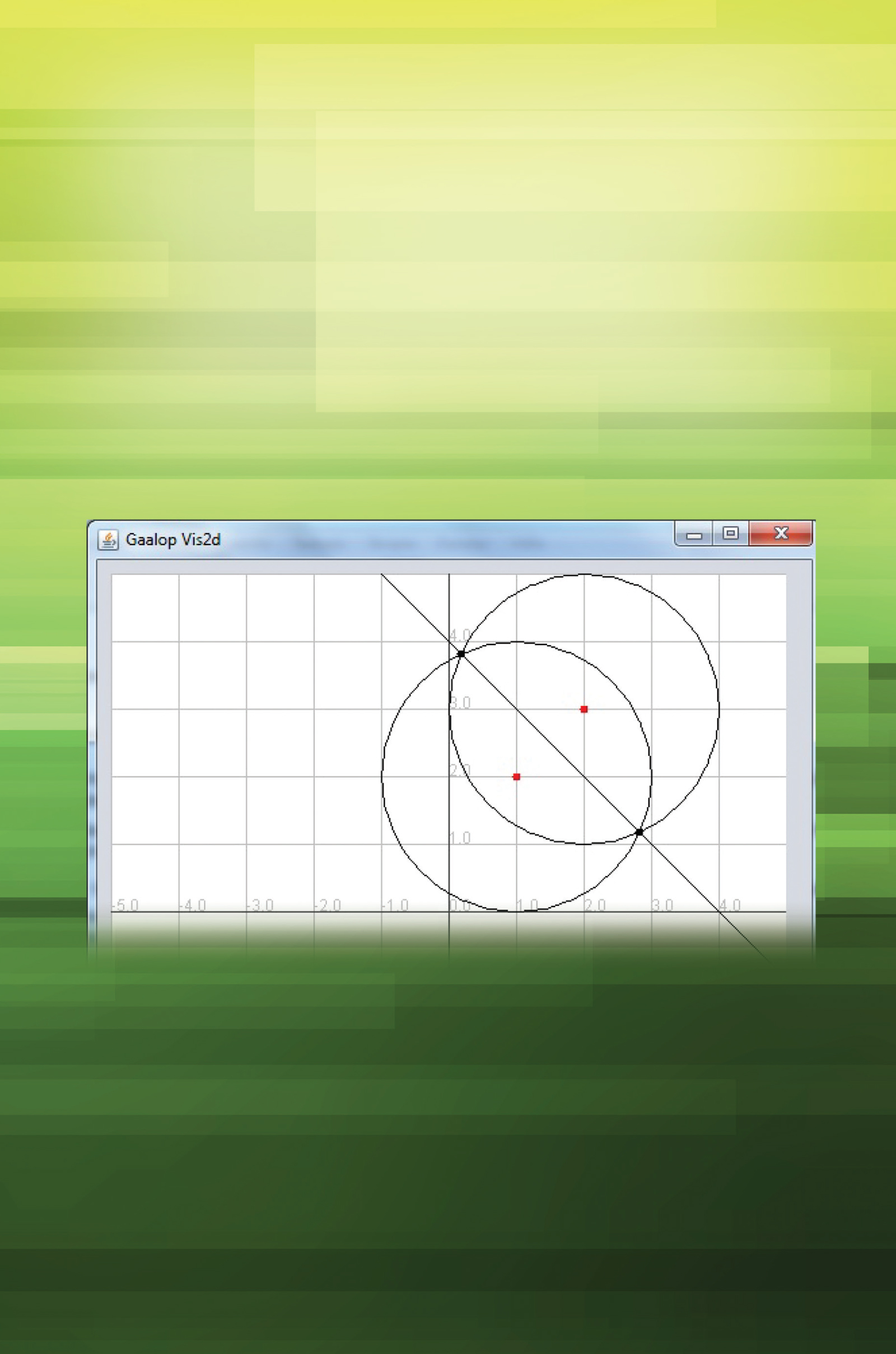
In geometric algebra, and especially so in conformal geometric algebra (CGA) of the two-dimensional plane, here appropriately named compass-ruler algebra (CRA), all expressions formed by elementary algebraic rules for addition and multiplication are geometrically meaningful and useful. This is beautifully shown in in the sections on difference and sum of two points, with respective interpretations as mid-line and circle (with the two points as poles), respectively.