CALCULUS
An Intuitive and Physical Approach
Morris Kline

SECOND EDITION
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 1967, 1977 by John Wiley & Sons, Inc.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 1998, is an unabridged republication of the work originally published in 1977 by John Wiley and Sons, Inc., New York.
Readers who would like to receive the solutions to the exercises may request them from the publisher at the following e-mail address:
Library of Congress Cataloging-in-Publication Data
Kline, Morris, 1908
Calculus : an intuitive and physical approach, second edition / Morris Kline.
p. cm.
An unabridged republication of the work originally published in 1977 by John Wiley and Sons, Inc., New YorkT.p. verso.
Includes index.
ISBN-13: 978-0-486-40453-0
ISBN-10: 0-486-40453-6
1. Calculus. I. Title.
QA303.K68 1998
515dc21
98-36211
CIP
Manufactured in the United States by Courier Corporation
40453609
www.doverpublications.com
Dedicated to the memory of
Morris Kline
19081992
Mathematician, Educator
PREFACE TO
THE SECOND EDITION
The basic features of the first edition have been retained, such as the intuitive approach and real applications. As to the approach, the last chapter introduces a rigorous treatment. Though this chapter could be used in conjunction with the opening chapters of the book, I do not recommend doing so; the rigorous presentation is difficult to grasp and obscures the understanding. Rigor undoubtedly refines the intuition but does not supplant it. The rigorous approach should be reserved for a course in advanced calculus for mathematicians.
Most of the applications still belong with the physical sciences; however, no knowledge of physics is presupposed. Several sections on physical applications have been dropped and applications to the social and biological sciences have been added instead. These applications are vital. The theory and technique of the calculus are, in themselves, meaningless. Moreover, since most students who take calculus will be scientists or engineers, they will be highly motivated by the applications. Many calculus texts dispose of applications by asking students to calculate centers of gravity and moments of inertia. But since students have no idea of how these quantities are used, the only consequence is that the gravity of the problems produces inertia in the students.
In addition to extending the scope of the applications, I have made a number of other improvements. More drill exercises have been added, the exercises have been carefully graded as to difficulty, and there are more illustrative examples. Students doing homework exercises acquire the habit of searching for an illustrative example which they can imitate and thereby do the exercises without thinking. To counter this many illustrative examples are incorporated into the text instead of being set apart formally. Hopefully the students will read the text instead of mechanically following the technique of the usual illustrative example.
A chapter on differential equations and a section on such numerical methods as Simpsons rule and the trapezoidal rule have also been added. More use has been made of vector analysis, particularly in treating velocity and acceleration.
, The Definite Integral, has been moved forward so that students using the mathematics in another course taken simultaneously can utilize the concept sooner.
Some changes in notation are unquestionably an improvement. The 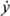 notation has been restricted to the customary situation where time is the independent variable; in other situations y, dy / dx and f(x) are used. The notation y dx has been introduced early to denote antidifferentiation. The use of dy / dx from the outset is the result of numerous requests. Admittedly, a useful notation in showing the variables involved, it also suggests that the derivative is a quotient, whereas we must take great pains to convince the student that it is not.
notation has been restricted to the customary situation where time is the independent variable; in other situations y, dy / dx and f(x) are used. The notation y dx has been introduced early to denote antidifferentiation. The use of dy / dx from the outset is the result of numerous requests. Admittedly, a useful notation in showing the variables involved, it also suggests that the derivative is a quotient, whereas we must take great pains to convince the student that it is not.
The pace of the first few chapters has been speeded up somewhat. However, it does seem desirable, because students are weak in algebra, to keep the algebra simple at the outset while students are acquiring the concepts of the calculus.
Two other changes may be helpful. Since not all classes go at the same pace or have the same objectives the two volumes of the first edition have been replaced by the present single volume. Thereby instructors are freer to choose the topics they deem most appropriate. Second, since time may not permit the inclusion of all the applications, those sections that can be omitted without disrupting the continuity have been starred.
Some figures have been improved; where the precise shape is significant the computer has been employed to achieve accuracy.
An instructors manual which contains full solutions of all the exercises, suggestions for teaching, and additional material for advanced students is available to instructors on request to the publisher.
Morris Kline
New York, N. Y.
August, 1976
PREFACE TO
THE FIRST EDITION
Anyone who adds to the plethora of introductory calculus texts owes an explanation, if not an apology, to the mathematical community. I believe that an introductory course in the calculus should present the subject intuitively and should relate it as closely as possible to science. A text for such an approach is not available.
In this book the justification of the theorems and techniques is consistently intuitive; that is, geometrical, physical, and heuristic arguments and generalizations from concrete cases are employed to convince. The approach is especially suitable for the calculus because the subject grew out of physical and geometrical problems. These problems tell us what functions we should take up, what concepts we want to formulate, and what techniques we should develop. In view of the fact that the human mind learns intuitively and that time does not permit both an intuitive and a rigorous presentation in elementary calculus, it seems to me that the approach adopted is the correct one.
The intuitive approach is explained to the student so that he will know what kind of evidence is being used to support arguments. Thus he is told that a graph of a typical function may not represent all functions. On the other hand, he is also told that the elementary functions are well behaved except at isolated points and that he can usually trust his intuition. As he works with the ideas of the calculus, he will sharpen his intuition. If he continues with mathematics, he will learn the analytical foundations and proofs that guard against the failings of intuition.
The use of an intuitive approach in the first treatment of a subject is not an innovation. Arithmetic is learned intuitively in elementary school and then the logic of it is learned gradually through the work in algebra. Geometry is learned intuitively in junior high school and then the formal deductive approach is presented in senior high school. A difficult subject such as the calculus, therefore, should certainly be introduced by an intuitive approach.
This approach has many merits beyond that of being the only feasible one. Every pedagogue today champions discovery, but few teach it. How does one discover in mathematics? By thinking in physical and geometrical terms, by conjecturing or guessing, by formulating hypotheses and testing them, and by generalizing on specific cases. Physical problems that call for the creation of mathematics set the stage for discovery. That the intuitive approach may lead to errors is granted, but truth emerges more readily from error than from confusion. The student must be allowed to make mistakes, for if he makes no mistakes, he will not progress.















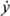 notation has been restricted to the customary situation where time is the independent variable; in other situations y, dy / dx and f(x) are used. The notation y dx has been introduced early to denote antidifferentiation. The use of dy / dx from the outset is the result of numerous requests. Admittedly, a useful notation in showing the variables involved, it also suggests that the derivative is a quotient, whereas we must take great pains to convince the student that it is not.
notation has been restricted to the customary situation where time is the independent variable; in other situations y, dy / dx and f(x) are used. The notation y dx has been introduced early to denote antidifferentiation. The use of dy / dx from the outset is the result of numerous requests. Admittedly, a useful notation in showing the variables involved, it also suggests that the derivative is a quotient, whereas we must take great pains to convince the student that it is not.