Narayanadash. - Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates
Here you can read online Narayanadash. - Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates
- Author:
- Genre:
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Narayanadash.: author's other books
Who wrote Ordinary and Partial Differentiation, Mean Value Theorems, Taylors Series, Orthogonal Coordinates? Find out the surname, the name of the author of the book and a list of all author's works by series.











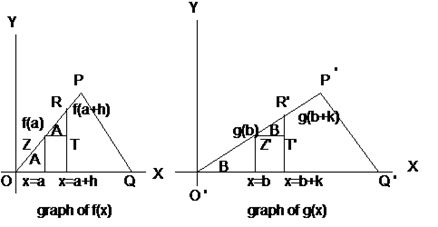 It is all about study of rates of change of functions . Functions may represent physical quantities, like say distance traveled from a point, then rate of change of distance with respect to time would represent another separate physical quantity, namely speed. If the physical quantity represents say, mass, rate of change with respect to volume would represent another physical quantity ,namely , density .If the physical quantity represents speed, its time rate of change would represent acceleration. If the quantity represents population, its rateof change with respect to area would represent population density.
It is all about study of rates of change of functions . Functions may represent physical quantities, like say distance traveled from a point, then rate of change of distance with respect to time would represent another separate physical quantity, namely speed. If the physical quantity represents say, mass, rate of change with respect to volume would represent another physical quantity ,namely , density .If the physical quantity represents speed, its time rate of change would represent acceleration. If the quantity represents population, its rateof change with respect to area would represent population density. 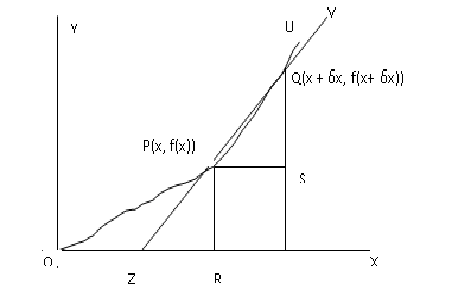 Because the hills were taken as straight, slope in one side remainedconstant from bottom to the top. Had the contour of the hill been like the curve OPQU as in the above figure ,we should consider a small distance PQ and measure the slope as QR/PR at the point P, for the slope is changing from point to point, the hill is more steep at some points and less at others. But how small an arc PQ is required for this purpose of measuring the slope ? The nearer Q is to P the better would be our approximation. We may afford to be exact theoretically, if we take ZPQV to be tangent to the curve instead of secant.
Because the hills were taken as straight, slope in one side remainedconstant from bottom to the top. Had the contour of the hill been like the curve OPQU as in the above figure ,we should consider a small distance PQ and measure the slope as QR/PR at the point P, for the slope is changing from point to point, the hill is more steep at some points and less at others. But how small an arc PQ is required for this purpose of measuring the slope ? The nearer Q is to P the better would be our approximation. We may afford to be exact theoretically, if we take ZPQV to be tangent to the curve instead of secant.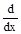 , or
, or 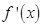 at x = a, written as
at x = a, written as 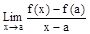 =
= 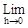
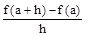 =
= 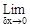
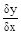 = tan (1), being the angle of the tangent of the curve at the point (x, f(x)) with the X-axis called the slope angle of the tangent QS of the curve at the point.. Note that the angle QPR = angle PSX = . We mean y as change in y, x as change in x, f as change inf(x), or, f(x+ x) - f(x). Further,note in the figure 3.1.a, that the slope of the line PO is +ve and that of PQ is ve, hence different. dy/dx being the limit of the slopes this limit here does not exist, as the left handed limit is different from the right handed limit. So derivative at a sharp point on a smooth curve does not exist.
= tan (1), being the angle of the tangent of the curve at the point (x, f(x)) with the X-axis called the slope angle of the tangent QS of the curve at the point.. Note that the angle QPR = angle PSX = . We mean y as change in y, x as change in x, f as change inf(x), or, f(x+ x) - f(x). Further,note in the figure 3.1.a, that the slope of the line PO is +ve and that of PQ is ve, hence different. dy/dx being the limit of the slopes this limit here does not exist, as the left handed limit is different from the right handed limit. So derivative at a sharp point on a smooth curve does not exist.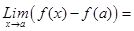
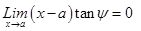 or
or 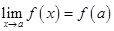 ;This is the criteria for the function to be continuous. So the function
;This is the criteria for the function to be continuous. So the function