Nathaniel Johnston - Advanced Linear and Matrix Algebra

Linear algebra, more so than any other mathematical subject, can be approached in numerous ways. Many textbooks present the subject in a very concrete and numerical manner, spending much of their time solving systems of linear equations and having students perform laborious row reductions on matrices. Many other books instead focus very heavily on linear transformations and other basis-independent properties, almost to the point that their connection to matrices is considered an inconvenient after-thought that students should avoid using at all costs.

This book is written from the perspective that both linear transformations and matrices are useful objects in their own right, but it is the connection between the two that really unlocks the magic of linear algebra. Sometimes when we want to know something about a linear transformation, the easiest way to get an answer is to grab onto a basis and look at the corresponding matrix. Conversely, there are many interesting families of matrices and matrix operations that seemingly have nothing to do with linear transformations, yet can nonetheless illuminate how some basis-independent objects and properties behave.

This book introduces many difficult-to-grasp objects such as vector spaces, dual spaces, and tensor products. Because it is expected that this book will accompany one of the first courses where students are exposed to such abstract concepts, we typically sandwich this abstractness between concrete examples. That is, we first introduce or emphasize a standard, prototypical example of the object to be introduced (e.g., 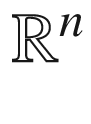), then we discuss its abstract generalization (e.g., vector spaces), and finally we explore other specific examples of that generalization (e.g., the vector space of polynomials and the vector space of matrices).

This book also delves somewhat deeper into matrix decompositions than most others do. We of course cover the singular value decomposition as well as several of its applications, but we also spend quite a bit of time looking at the Jordan decomposition, Schur triangularization, and spectral decomposition, and we compare and contrast them with each other to highlight when each one is appropriate to use. Computationally-motivated decompositions like the QR and Cholesky decompositions are also covered in some of this books many Extra Topic sections.

This book is the second part of a two-book series, following the book Introduction to Linear and Matrix Algebra [Joh20]. The reader is expected to be familiar with the basics of linear algebra covered in that book (as well as other introductory linear algebra books): vectors in 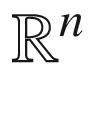, the dot product, matrices and matrix multiplication, Gaussian elimination, the inverse, range, null space, rank, and determinant of a matrix, as well as eigenvalues and eigenvectors. These preliminary topics are briefly reviewed in Appendix A.1.

Because these books aim to not overlap with each other and repeat content, we do not discuss some topics that are instead explored in that book. In particular, diagonalization of a matrix via its eigenvalues and eigenvectors is discussed in the introductory book and not here. However, many extensions and variations of diagonalization, such as the spectral decomposition (Section ) are explored here.

This book makes use of numerous features to make it as easy to read and understand as possible. Here we highlight some of these features and discuss how to best make use of them.

This text makes heavy use of notes in the margin, which are used to introduce some additional terminology or provide reminders that would be distracting in the main text. They are most commonly used to try to address potential points of confusion for the reader, so it is best not to skip them.

For example, if we want to clarify why a particular piece of notation is the way it is, we do so in the margin so as to not derail the main discussion. Similarly, if we use some basic fact that students are expected to be aware of (but have perhaps forgotten) from an introductory linear algebra course, the margin will contain a brief reminder of why its true.

Several exercises can be found at the end of every section in this book, and whenever possible there are three types of them: