Handbook of the History of Logic, Vol. 6, suppl (C), 2012
ISSN: 1874-5857
doi: 10.1016/B978-0-444-51621-3.50012-8
Front matter
Handbook of the History of Logic, Vol. 6, suppl (C), 2012
ISSN: 1874-5857
doi: 10.1016/B978-0-444-51621-3.50013-X
Copyright
Handbook of the History of Logic, Vol. 6, suppl (C), 2012
ISSN: 1874-5857
doi: 10.1016/B978-0-444-51621-3.50014-1
Preface
Handbook of the History of Logic, Vol. 6, suppl (C), 2012
ISSN: 1874-5857
doi: 10.1016/B978-0-444-51621-3.50015-3
Contributors
Handbook of the History of Logic, Vol. 6, suppl (C), 2012
ISSN: 1874-5857
doi: 10.1016/B978-0-444-51621-3.50001-3
Set Theory from Cantor to Cohen
Akihiro Kanamori
Set theory is an autonomous and sophisticated field of mathematics, enormously successful not only at its continuing development of its historical heritage but also at analyzing mathematical propositions and gauging their consistency strength. But set theory is also distinguished by having begun intertwined with pronounced metaphysical attitudes, and these have even been regarded as crucial by some of its great developers. This has encouraged the exaggeration of crises in foundations and of metaphysical doctrines in general. However, set theory has proceeded in the opposite direction, from a web of intensions to a theory of extension par excellence, and like other fields of mathematics its vitality and progress have depended on a steadily growing core of mathematical proofs and methods, problems and results. There is also the stronger contention that from the beginning set theory actually developed through a progression of mathematical moves, whatever and sometimes in spite of what has been claimed on its behalf.
What follows is an account of the development of set theory from its beginnings through the creation of forcing based on these contentions, with an avowedly Whiggish emphasis on the heritage that has been retained and developed by the current theory. The whole transfinite landscape can be viewed as having been articulated by Cantor in significant part to solve the Continuum Problem. Zermelos axioms can be construed as clarifying the set existence commitments of a single proof, of his Well-Ordering Theorem. Set theory is a particular case of a field of mathematics in which seminal proofs and pivotal problems actually shaped the basic concepts and forged axiomatizations, these transmuting the very notion of set. There were two main junctures, the first being when Zermelo through his axiomatization shifted the notion of set from Cantors range of inherently structured sets to sets solely structured by membership and governed and generated by axioms. The second juncture was when the Replacement and Foundation Axioms were adjoined and a first-order setting was established; thus transfinite recursion was incorporated and results about all sets could established through these means, including results about definability and inner models. With the emergence of the cumulative hierarchy picture, set theory can be regarded as becoming a theory of well-foundedness, later to expand to a study of consistency strength. Throughout, the subject has not only been sustained by the axiomatic tradition through Gdel and Cohen but also fueled by Cantors two legacies, the extension of number into the transfinite as transmuted into the theory of large cardinals and the investigation of definable sets of reals as transmuted into descriptive set theory. All this can be regarded as having a historical and mathematical logic internal to set theory, one that is often misrepresented at critical junctures in textbooks (as will be pointed out). This view, from inside set theory and about itself, serves to shift the focus to those tensions and strategies familiar to mathematicians as well as to those moves, often made without much fanfare and sometimes merely linguistic, that have led to the crucial advances.
Cantor
1.1 Real numbers and countability
Set theory had its beginnings in the great 19th-Century transformation of mathematics, a transformation beginning in analysis. Since the creation of the calculus by Newton and Leibniz the function concept had been steadily extended from analytic expressions toward arbitrary correspondences. The first major expansion had been inspired by the explorations of Euler in the 18th Century and featured the infusion of infinite series methods and the analysis of physical phenomena, like the vibrating string. In the 19th-Century the stress brought on by the unbridled use of series of functions led first Cauchy and then Weierstrass to articulate convergence and continuity. With infinitesimals replaced by the limit concept and that cast in the - language, a level of deductive rigor was incorporated into mathematics that had been absent for two millenia. Sense for the new functions given in terms of infinite series could only be developed through carefully specified deductive procedures, and proof reemerged as an extension of algebraic calculation and became basic to mathematics in general, promoting new abstractions and generalizations.
It was in [1872] that Cantor provided his formulation of the real numbers in terms of fundamental sequences of rational numbers, and significantly, this was for the specific purpose of articulating his proof. With the new results of analysis to be secured by proof and proof in turn to be based on prior principles the regress led in the early 1870s to the appearance of several independent formulations of the real numbers in terms of the rational numbers. It is at first quite striking that the real numbers came to be developed so late, but this can be viewed as part of the expansion of the function concept which shifted the emphasis from the continuum taken as a whole to its extensional construal as a collection of objects. In mathematics objects have been traditionally introduced only with reluctance, but a more arithmetical rather than geometrical approach to the continuum became necessary for the articulation of proofs.
The algebraic numbers would soon be the focus of a major breakthrough by Cantor. Although both Cantor and Dedekind carried out an arithmetical reduction of the continuum, they each accommodated its antecedent geometric sense by asserting that each of their real numbers actually corresponds to a point on the line. Neither theft nor honest toil sufficed; Cantor [1872:128] and Dedekind [1872:III] recognized the need for an axiom to this effect, a sort of Churchs Thesis of adequacy for the new construal of the continuum as a collection of objects.
that around this time he was already considering infinite iterations of his P operation using symbols of infinity:
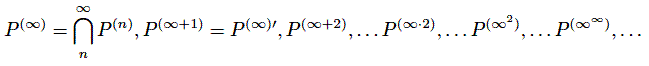
In the next decades the subject was to blossom through the prodigious progress made by him in the theory of transfinite and cardinal numbers.
The uncountability of the reals was established, of course, via reductio ad absurdum as with the irrationality of 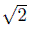 . Both impossibility results epitomize how a reductio can compel a larger mathematical context allowing for the deniability of hitherto implicit properties. Be that as it may, Cantor the mathematician addressed a specific problem, embedded in the mathematics of the time, in his seminal [1874] entitled On a property of the totality of all real algebraic numbers. After first establishing this property, the countability of the algebraic numbers, Cantor then established:
. Both impossibility results epitomize how a reductio can compel a larger mathematical context allowing for the deniability of hitherto implicit properties. Be that as it may, Cantor the mathematician addressed a specific problem, embedded in the mathematics of the time, in his seminal [1874] entitled On a property of the totality of all real algebraic numbers. After first establishing this property, the countability of the algebraic numbers, Cantor then established:













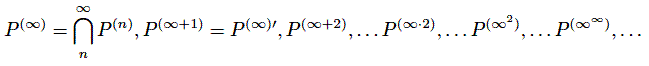
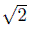 . Both impossibility results epitomize how a reductio can compel a larger mathematical context allowing for the deniability of hitherto implicit properties. Be that as it may, Cantor the mathematician addressed a specific problem, embedded in the mathematics of the time, in his seminal [1874] entitled On a property of the totality of all real algebraic numbers. After first establishing this property, the countability of the algebraic numbers, Cantor then established:
. Both impossibility results epitomize how a reductio can compel a larger mathematical context allowing for the deniability of hitherto implicit properties. Be that as it may, Cantor the mathematician addressed a specific problem, embedded in the mathematics of the time, in his seminal [1874] entitled On a property of the totality of all real algebraic numbers. After first establishing this property, the countability of the algebraic numbers, Cantor then established: